
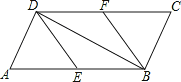
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
【答案】(1)证明见解析;(2)若∠ADB是直角,则四边形BEDF是菱形,理由见解析.
【解析】试题(1)由四边形ABCD是平行四边形,即可得AD=BC,AB=CD,∠A=∠C,又由E、F分别为边AB、CD的中点,可证得AE=CF,然后由SAS,即可判定△ADE≌△CBF;
(2)先证明BE与DF平行且相等,然后根据一组对边平行且相等的四边形是平行四边形,再连接EF,可以证明四边形AEFD是平行四边形,所以AD∥EF,又AD⊥BD,所以BD⊥EF,根据菱形的判定可以得到四边形是菱形.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD,
CD,
∴AE=CF,
在△ADE和△CBF中,
 ,
,
∴△ADE≌△CBF(SAS);
(2)若∠ADB是直角,则四边形BEDF是菱形,理由如下:
解:由(1)可得BE=DF,
又∵AB∥CD,
∴BE∥DF,BE=DF,
∴四边形BEDF是平行四边形,
连接EF,在ABCD中,E、F分别为边AB、CD的中点,
∴DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∴EF∥AD,
∵∠ADB是直角,
∴AD⊥BD,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系. 
(1)分别求出该材料加热过程中和停止加热后y与x之间的函数表达式,并写出x的取值范围;
(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )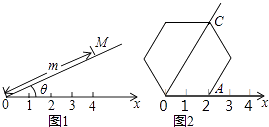
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一次函数y=kx+b的图象,以下说法中正确的是( )

A. 直线与y轴的交点为(3,0) B. y随x的增大而增大
C. 直线与两坐标轴围成的三角形面积是6 D. 一元一次方程kx+b=0的解为x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题:①若 ![]() =
= ![]() ,则tan∠EDF=
,则tan∠EDF= ![]() ;②若DE2=BDEF,则DF=2AD,则( )
;②若DE2=BDEF,则DF=2AD,则( ) 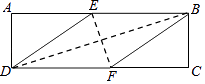
A.①是假命题,②是假命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是真命题,②是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题
(1)某中学组织初一学生春游,原计划租用45座汽车若干辆,但有15人没有座位;若租用同样数量的60座汽车,则比45座汽车多出一辆无人乘坐,但其余客车恰好坐满.问初一年级人数是多少?原计划租用45座汽车多少辆?
(2)《孙子算经》是中国古代重要的数学著作,记有许多有趣而又不乏技巧的算术程式,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八.乙得甲太半,亦满四十八,问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲,乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲,乙二人原来各有多少钱?”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com