
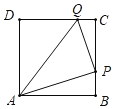
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)8;(2)BP=![]() ;(3)
;(3)![]() ;(4)S
;(4)S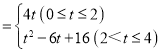 .
.
【解析】
(1)先确定当t=2时P和Q的位置,再利用三角形面积公式可得结论;
(2)分两种情况表示BP的长;
(3)如图2,根据CQ=CP列方程可解答;
(4)分两种情况:
①当0≤t≤2时,P在AB上,如图3,②当2<t≤4时,P在BC上,如图4,根据三角形面积公式可得结论.
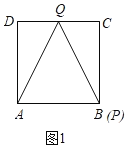
(1)当t=2时,点P与B重合,Q在CD上,如图1,∴△APQ的面积![]() 8(平方厘米).
8(平方厘米).
故答案为:8;
(2)分两种情况:
当0≤t≤2时,P在AB上,BP=AB﹣AP=4﹣2t,当2<t≤4时,P在BC上,BP=2t﹣4;
综上所述:BP=![]() ;
;
(3)如图2.
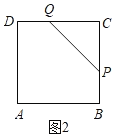
∵△PCQ为等腰三角形,∴CQ=CP,即t=8﹣2t,t![]() ,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是
,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是![]() 秒;
秒;
(4)分两种情况:
①当0≤t≤2时,P在AB上,如图3.
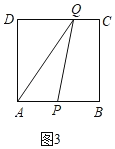
S![]() 4t
4t
②当2<t≤4时,P在BC上,如图4.
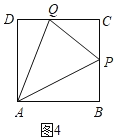
S=S正方形ABCD﹣S△ABP﹣S△CPQ﹣S△ADQ=4×4![]() t2﹣6t+16;
t2﹣6t+16;
综上所述:S与t之间的函数关系式为:S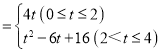 .
.


科目:初中数学 来源: 题型:
【题目】如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
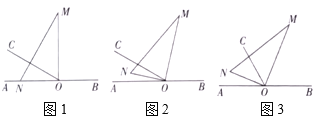
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过![]() 秒后,边
秒后,边![]() 恰好平分
恰好平分![]() .求
.求![]() 的值;
的值;
(2)在(1)问条件的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
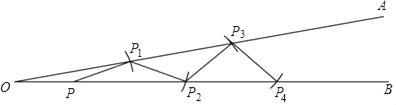
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北国超市销售每台进价分别为400元、350元的![]() 两种型号的豆浆机.下表是近两周的销售情况:
两种型号的豆浆机.下表是近两周的销售情况:
销售数量:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 5台 | 3500元 |
第二周 | 4台 | 10台 | 6000元 |
(进价、售价均保持不变,利润=销售收入-进价)
(1)求![]() 两种型号的豆浆机的销售单价;
两种型号的豆浆机的销售单价;
(2 )若第三周该超市采购这两种型号的豆浆机共20台, 并且B型号的台数比A型号的台数的2倍少1 ,如果这20台豆浆机全部售出,求这周销售的利润;
(3)若恰好用8000元采购这两种型号的豆浆机,问有哪几种进货方案? ( 要求两种型号都要采购)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
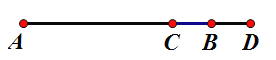
(1)图中共有______条线段,分别是______;
(2)求线段![]() 的长;
的长;
(3)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() .
.
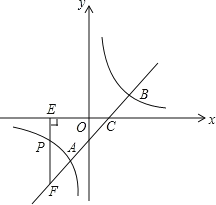
(1)求反比例函数的解析式;
(2)若点![]() 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
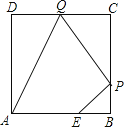
A. 3 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
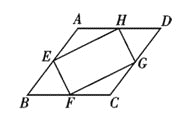
【题目】如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )
A. ![]() B. 2
B. 2 ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
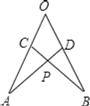
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com