
【题目】如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
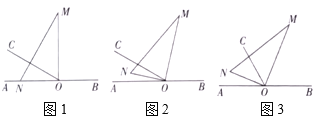
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过![]() 秒后,边
秒后,边![]() 恰好平分
恰好平分![]() .求
.求![]() 的值;
的值;
(2)在(1)问条件的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
【答案】(1)5秒;(2)5秒时OC平分∠MON,理由见解析
【解析】
(1)由OM平分∠BOC,得∠COM=∠MOB,结合∠AOC=30°,得∠COM=75°,进而得∠AON=15°,即可得到答案;
(2)由三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,得∠AON=3t,∠AOC=30°+6t,由OC平分∠MON,得∠CON=∠COM=45°,进而列出关于t的方程,即可求解.
(1)∵∠AON+∠MON+∠BOM=180°,∠MON=90°,
∴∠AON+∠BOM=90°,
∵OM平分∠BOC,
∴∠COM=∠MOB,
∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC-∠CON=30°-15°=15°,
∴t=15÷3=5秒;
(2)经过5秒时,OC平分∠MON,理由如下:
∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
∴∠AON=3t,∠AOC=30°+6t,
∵∠AOC-∠AON=45°,
∴30°+6t-3t=45°,
解得:t=5秒;


科目:初中数学 来源: 题型:
【题目】某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)α= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
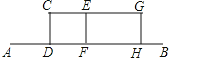
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知∠1与线段a,用直尺和圆规按下列步骤作图(保留作图痕迹,不写做法。)
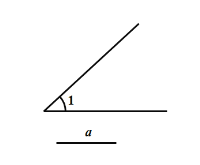
(1)作等∠A于∠1
(2)在∠A的两边分别作AM=AN=a
(3)连接MN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格图由边长为1的小正方形所构成,Rt△ABC的顶点分别是A(-1,3),B(-3,-1),C(-3,3).

(1)请在图1中作出△ABC关于点(-1,0)成中心对称△![]() ,并分别写出A,C对应点的坐标
,并分别写出A,C对应点的坐标![]() ;
;![]()
(2)设线段AB所在直线的函数表达式为![]() ,试写出不等式
,试写出不等式![]() 的解集是 ;
的解集是 ;
(3)点M和点N 分别是直线AB和y轴上的动点,若以![]() ,
,![]() ,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,点D在边BC上
,点D在边BC上![]() 与B,C不重合
与B,C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:![]() ;
;![]() :2;
:2;![]() ;
;![]() 其中正确结论的个数是
其中正确结论的个数是![]()
![]()
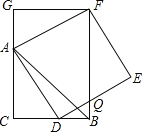
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
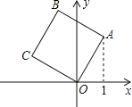
A. (﹣2,1)B. (﹣1,2)C. (![]() ,﹣1)D. (﹣
,﹣1)D. (﹣![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角![]() 和
和![]() 有公共顶点
有公共顶点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③若
;③若![]() 平分
平分![]() ,则
,则![]() 平分
平分![]() ;④
;④![]() 的平分线与
的平分线与![]() 的平分线是同一条射线.其中结论正确的个数是( )
的平分线是同一条射线.其中结论正确的个数是( )
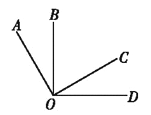
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
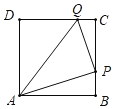
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com