
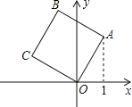
【题目】如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A. (﹣2,1)B. (﹣1,2)C. (![]() ,﹣1)D. (﹣
,﹣1)D. (﹣![]() ,1)
,1)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】12月4日为全国法制宣传日,当天某初中组织4名学生参加法制知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录了其中2名参赛学生的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 17 | 3 | 79 |
(1)参赛学生![]() 得72分,他答对了几道题?答错了几道题?
得72分,他答对了几道题?答错了几道题?
(2)参赛学生![]() 说他可以得88分,你认为可能吗?为什么?
说他可以得88分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
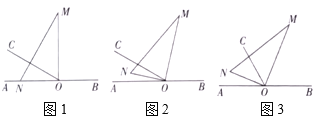
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过![]() 秒后,边
秒后,边![]() 恰好平分
恰好平分![]() .求
.求![]() 的值;
的值;
(2)在(1)问条件的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
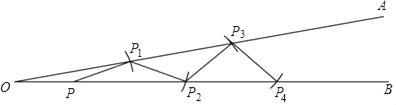
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
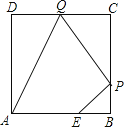
A. 3 B. 5 C. 4 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com