
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
【答案】D
【解析】
由题意,在此过程中这四种情形的可能:(1)快车未出发时,两车相距![]() ;(2)快车追赶慢车时,两车相距
;(2)快车追赶慢车时,两车相距![]() ;(3)快车已反超慢车但未达到乙地时,两车相距
;(3)快车已反超慢车但未达到乙地时,两车相距![]() ;(4)快车到达乙地,慢车行驶了
;(4)快车到达乙地,慢车行驶了![]() 时,两车相距
时,两车相距![]() .再根据两车的速度分析时间上是否匹配即可.
.再根据两车的速度分析时间上是否匹配即可.
设快车行驶的时间为![]() 小时
小时
依题意有以下四种情形:
(1)快车未出发时,即![]() 时,慢车行驶了
时,慢车行驶了![]() 小时,两车恰好相距
小时,两车恰好相距![]()
(2)快车已出发,开始追赶慢车时
则![]() 解得:
解得:![]()
此时慢车行驶了![]() ,快车行驶了
,快车行驶了![]() ,两车恰好相距
,两车恰好相距![]()
(3)快车已反超慢车但未达到乙地时
则![]() 解得:
解得:![]()
此时慢车行驶了![]() ,快车行驶了
,快车行驶了![]() ,两车恰好相距
,两车恰好相距![]()
(4)快车到达乙地,慢车行驶了![]() 时
时
则![]() 解得:
解得:![]()
此时快车行驶了![]() ,慢车行驶了
,慢车行驶了![]() ,两车相距
,两车相距![]() ;在这之后,慢车继续行驶
;在这之后,慢车继续行驶![]() 小时,也就是再行驶
小时,也就是再行驶![]() 至
至![]() 处,这时候两车恰好相距
处,这时候两车恰好相距![]()
综上,以上四种情形均符合,即在此过程中,两车恰好相距![]() 的次数是4
的次数是4
故答案为:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点A、C均在坐标轴上,且OA=4,OC=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC于点P,连接MP.

(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
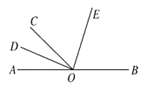
【题目】已知![]() 、
、![]() 、
、![]() 三点在同一条直线上,
三点在同一条直线上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)![]() 是否随
是否随![]() 的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF。
(1)若DE=DC,求证:四边形CDEF是菱形;
(2)若AB=![]() ,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。
,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,抛物线![]() 的图像与x轴交于点A(3,0),与y轴交于点B,顶点C在直线
的图像与x轴交于点A(3,0),与y轴交于点B,顶点C在直线![]() 上,将抛物线沿射线 AC的方向平移,
上,将抛物线沿射线 AC的方向平移,
当顶点C恰好落在y轴上的点D处时,点B落在点E处.
(1)求这个抛物线的解析式;
(2)求平移过程中线段BC所扫过的面积;
(3)已知点F在x轴上,点G在坐标平面内,且以点 C、E、F、G 为顶点的四边形是矩形,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油.在此次行驶过程中,行驶了450千米时,司机发现离前方最近的加油站有75千米的路程.在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com