
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油.在此次行驶过程中,行驶了450千米时,司机发现离前方最近的加油站有75千米的路程.在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是多少千米?

【答案】(1)该一次函数解析式为y=![]() x+60;(2)离加油站的路程是10千米.
x+60;(2)离加油站的路程是10千米.
【解析】
(1)分析题意,首先根据函数图象中点的坐标利用待定系数法求出一次函数解析式;
(2)根据一次函数图象上点的坐标特征即可求出剩余油量为8升时行驶的路程,用总路程减去剩余油量为8升时行驶的路程即可解答本题。
(1)设该一次函数解析式为y=kx+b,
将(150,45)、(0,60)代入y=kx+b中,得![]() ,
,
解得: ,
,
∴该一次函数解析式为y=![]() x+60.
x+60.
(2)当y=![]() x+60=8时,
x+60=8时,
解得x=520.
即行驶520千米时,油箱中的剩余油量为8升.
530-520=10千米,
油箱中的剩余油量为8升时,距离加油站10千米.
∴在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是10千米.


科目:初中数学 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△DCE都是等腰直角三角形,CA=CB,CD=CE,∠ACB=∠DCE=90°,△ACB的顶点A在△DCE的斜边DE上,且AD=![]() ,AE=3
,AE=3![]() ,则AC=_____.
,则AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=![]() BC,求线段PQ的长.
BC,求线段PQ的长.
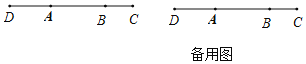
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决后面三个问题:
我们可以将任意三位数表示为![]() (其中a、b、c分别表示百位上的数字,十位上的数字和个位上的数字,且a ≠0),显然
(其中a、b、c分别表示百位上的数字,十位上的数字和个位上的数字,且a ≠0),显然![]() =100a +10b +c;我们形如
=100a +10b +c;我们形如![]() 和
和![]() 的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对姊妹数,678和876是一对“姊妹数”。
的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对姊妹数,678和876是一对“姊妹数”。
(1)写出任意两对“姊妹数”。
(2)一对“姊妹数”的和为1110,求这对“姊妹数”。
(3)如果用x表示百位数字,求证:任意一对“姊妹数”的和能被37整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形![]() 放入平面直角坐标系
放入平面直角坐标系![]() 中,使
中,使![]() 分别落在
分别落在![]() 轴的正半轴上,其中
轴的正半轴上,其中![]() ,对角线
,对角线![]() 所在直线解析式为
所在直线解析式为![]() ,将矩形
,将矩形![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 上的
上的![]() 处.
处.

(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的长度;
的长度;
(3)点![]() 是
是![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() 使得
使得![]() 的周长最小,若存在,请求出点
的周长最小,若存在,请求出点![]() 的坐标,如不存在,请说明理由.
的坐标,如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张在自家土地上平整出了一块苗圃,并将这块苗圃分成了四个长方形区域,其尺寸如图所示(图中长度单位:米),小张计划在这四个区域上按图中所示分别种植草本花卉 1 号、2 号、3 号、4 号.
(1)用式子表示这块苗圃的总面积;
(2)已知种植草本花卉 1 号、2 号、3 号、4 号的成本分别是每平方米 4 元、6 元、8 元、10 元.
①用式子表示小张在这块苗圃上种植草本花卉的总成本;
②当 a=9 时,求小张在这块苗圃上种植草本花卉的总成本.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com