
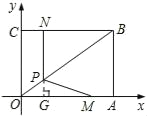
ЎѕМвДїЎїИзНјЈ¬ФЪЦ±ЅЗЧш±кПµЦРЈ¬ѕШРОOABCµД¶ҐµгAЎўCѕщФЪЧш±кЦбЙПЈ¬ЗТOA=4Ј¬OC=3Ј¬¶ЇµгMґУµгAіц·ўЈ¬ТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИЈ¬СШAOПтЦХµгOТЖ¶ЇЈ»¶ЇµгNґУµгCіц·ўСШCBПтЦХµгBТФН¬СщµДЛЩ¶ИТЖ¶ЇЈ¬µ±БЅёц¶ЇµгФЛ¶ЇБЛxГлЈЁ0ЈјxЈј4Ј©К±Ј¬№эµгNЧчNPЎНBCУЪµгPЈ¬Б¬ЅУMPЈ®

ЈЁ1Ј©Ц±ЅУРґіцµгBµДЧш±кЈ¬ІўЗуіцµгPµДЧш±кЈЁУГє¬xµДКЅЧУ±нКѕЈ©Ј»
ЈЁ2Ј©ЙиЎчOMPµДГж»эОЄSЈ¬ЗуSУлxЦ®јдµДєЇКэ±нґпКЅЈ»µ±xОЄєОЦµК±Ј¬SУРЧоґуЦµЈїЧоґуЦµКЗ¶аЙЩЈї
ЈЁ3Ј©ФЪБЅёц¶ЇµгФЛ¶ЇµД№эіМЦРЈ¬КЗ·сґжФЪДіТ»К±їМЈ¬К№ЎчOMPКЗµИСьИэЅЗРОЈїИфґжФЪЈ¬ЗуіцxµДЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©BµгЧш±кОЄЈЁ4Ј¬3Ј©Ј®µгPµДЧш±кОЄЈЁxЈ¬![]() xЈ©Ј»ЈЁ2Ј©µ±x=2К±Ј¬SУРЧоґуЦµЈ¬ЧоґуЦµОЄ
xЈ©Ј»ЈЁ2Ј©µ±x=2К±Ј¬SУРЧоґуЦµЈ¬ЧоґуЦµОЄ![]() Ј»(3) MµДЧш±кОЄЈЁ
Ј»(3) MµДЧш±кОЄЈЁ![]() Ј¬0Ј©»тЈЁ
Ј¬0Ј©»тЈЁ![]() Ј¬0Ј©»тЈЁ
Ј¬0Ј©»тЈЁ![]() Ј¬0Ј©Ј®
Ј¬0Ј©Ј®
ЎѕЅвОцЎї
КФМв·ЦОцЈєЈЁ1Ј©ёщѕЭѕШРОOABCЦРOA=4Ј¬OC=3ТФј°ѕШРОµДРФЦКЈ¬µГіцBµгЧш±кЈ¬ФЩУЙPGЎОABЈ¬µГіцЎчOPGЎЧЎчOBAЈ¬АыУГПаЛЖИэЅЗРО¶ФУ¦±ЯіЙ±ИАэµГіцPµгЧш±кЈ»
ЈЁ2Ј©АыУГPGТФј°OMµДі¤±нКѕіцЎчOMPµДГж»эЈ¬ФЩёщѕЭ¶юґОєЇКэµДРФЦКЗуіцЧоґуЦµјґїЙЈ»
ЈЁ3Ј©ЎчOMPКЗµИСьИэЅЗРОК±Ј¬·ЦИэЦЦЗйїцЈєўЩPO=PMЈ»ўЪOP=OMЈ»ўЫOM=PMЈ®»іцНјРОЈ¬·Ц±рЗуіцјґїЙЈ®
КФМвЅвОцЈєЈЁ1Ј©ЎЯѕШРОOABCЦРЈ¬OA=4Ј¬OC=3Ј¬
ЎаBµгЧш±кОЄЈЁ4Ј¬3Ј©Ј®
ИзНјЈ¬СУі¤NPЈ¬Ѕ»OAУЪµгGЈ¬ФтPGЎОABЈ¬OG=CN=xЈ®
ЎЯPGЎОABЈ¬
ЎаЎчOPGЎЧЎчOBAЈ¬
Ўа![]() Ј¬јґ
Ј¬јґ![]() Ј¬ЅвµГPG=
Ј¬ЅвµГPG=![]() xЈ¬
xЈ¬
ЎаµгPµДЧш±кОЄЈЁxЈ¬![]() xЈ©Ј»
xЈ©Ј»
ЈЁ2Ј©ЎЯФЪЎчOMPЦРЈ¬OM=4-xЈ¬OM±ЯЙПµДёЯОЄ![]() xЈ¬
xЈ¬
ЎаS=![]() ЈЁ4-xЈ©
ЈЁ4-xЈ©![]() x=-
x=-![]() x2+
x2+![]() xЈ¬
xЈ¬
ЎаSУлxЦ®јдµДєЇКэ±нґпКЅОЄS=-![]() x2+
x2+![]() xЈЁ0ЈјxЈј4Ј©Ј®
xЈЁ0ЈјxЈј4Ј©Ј®
Ед·ЅЈ¬µГS=-![]() ЈЁx-2Ј©2+
ЈЁx-2Ј©2+![]() Ј¬
Ј¬
Ўаµ±x=2К±Ј¬SУРЧоґуЦµЈ¬ЧоґуЦµОЄ![]() Ј»
Ј»
ЈЁ3Ј©ґжФЪДіТ»К±їМЈ¬К№ЎчOMPКЗµИСьИэЅЗРОЈ®АнУЙИзПВЈє
ўЩИз±ёУГНј1Ј¬

ИфPO=PMЈ¬ФтOG=GM=CN=xЈ¬
јґ3x=4Ј¬ЅвµГЈєx=![]() Ј¬
Ј¬
ЛщТФMЈЁ![]() Ј¬0Ј©Ј»
Ј¬0Ј©Ј»
ўЪИз±ёУГНј2Ј¬

ИфOP=OMЈ¬Фт![]() =OMЈ¬
=OMЈ¬
јґ![]() x=4-xЈ¬ЅвµГЈєx=
x=4-xЈ¬ЅвµГЈєx=![]() Ј¬
Ј¬
ЛщТФMЈЁ![]() Ј¬0Ј©Ј»
Ј¬0Ј©Ј»
ўЫИз±ёУГНј3Ј¬

ИфOM=PMК±Ј¬
ЎЯPG=![]() xЈ¬GM=OM-OG=ЈЁ4-xЈ©-x=4-2xЈ¬
xЈ¬GM=OM-OG=ЈЁ4-xЈ©-x=4-2xЈ¬
ЎаPM2=PG2+GM2=ЈЁ![]() xЈ©2+ЈЁ4-2xЈ©2Ј¬
xЈ©2+ЈЁ4-2xЈ©2Ј¬
ЎЯOM=4-xЈ¬
ЎаЈЁ4-xЈ©2=ЈЁ![]() xЈ©2+ЈЁ4-2xЈ©2Ј¬ЅвµГЈєx=
xЈ©2+ЈЁ4-2xЈ©2Ј¬ЅвµГЈєx=![]() Ј¬
Ј¬
ЛщТФЈ¬MЈЁ![]() Ј¬0Ј©Ј®
Ј¬0Ј©Ј®
ЧЫЙПЛщКцЈ¬MµДЧш±кОЄЈЁ![]() Ј¬0Ј©»тЈЁ
Ј¬0Ј©»тЈЁ![]() Ј¬0Ј©»тЈЁ
Ј¬0Ј©»тЈЁ![]() Ј¬0Ј©Ј®
Ј¬0Ј©Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЙъ»оЦРЈ¬ИЛГЗѕіЈНЁ№эТ»Р©±кЦѕРФЅЁЦюИ·¶ЁО»ЦГЈ¬ФЪКэС§ЦРНщНщТІКЗХвСщЈ®
ЈЁ1Ј©Ѕ«ХэХыКэИзНј1µД·ЅКЅЅшРРЕЕБРЈє

РЎГчН¬С§НЁ№эЧРПё№ЫІмЈ¬·ўПЦГїТ»РРµЪТ»БРµДКэЧЦУРТ»¶ЁµД№жВЙЈ¬ЛщТФГїТ»РРµЪТ»БРµДКэЧЦїЙТФЧчОЄ±кЦѕКэЈ¬УЪКЗЛыИПОЄµЪЖЯРРµЪТ»БРµДКэЧЦКЗЎЎ ЎЎЈ¬µЪ7РРЎўµЪ5БРµДКэЧЦКЗЎЎ ЎЎЈ®
ЈЁ2Ј©·Ѕ·ЁУ¦УГ
№ЫІмПВГжТ»БРКэЈє1Ј¬©Ѓ2Ј¬3Ј¬©Ѓ4Ј¬5Ј¬©Ѓ6Ј¬7Ј¬ЎІўЅ«ХвБРКэ°ґХХИзНј2·ЅКЅЅшРРЕЕБРЈє
°ґХХЙПКц·ЅКЅЕЕБРПВИҐЈ¬
ОКМв1ЈєµЪ10РРґУЧу±ЯКэµЪ9ёцКэКЗЎЎ ЎЎЈ»
ОКМв2ЈєµЪnРРУРЎЎ ЎЎёцКэЈ»ЈЁУГє¬nµДґъКэКЅ±нКѕЈ©
ОКМв3ЈєКэЧЦ2019ФЪµЪЎЎ ЎЎРРЈ¬ґУЧу±ЯКэµЪЎЎ ЎЎёцКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРГьМвЈєўЩИфaЈј1Ј¬ФтЈЁa©Ѓ1Ј©![]() =©Ѓ
=©Ѓ![]() Ј»ўЪФІКЗЦРРД¶ФіЖНјРОУЦКЗЦб¶ФіЖНјРОЈ»ўЫ
Ј»ўЪФІКЗЦРРД¶ФіЖНјРОУЦКЗЦб¶ФіЖНјРОЈ»ўЫ![]() µДЛгКхЖЅ·ЅёщКЗ4Ј»ўЬИз№ы·ЅіМax2+2x+1=0УРКµКэёщЈ¬ФтКµКэaЎЬ1Ј®ЖдЦРХэИ·µДГьМвёцКэКЗЈЁЎЎЎЎЈ©
µДЛгКхЖЅ·ЅёщКЗ4Ј»ўЬИз№ы·ЅіМax2+2x+1=0УРКµКэёщЈ¬ФтКµКэaЎЬ1Ј®ЖдЦРХэИ·µДГьМвёцКэКЗЈЁЎЎЎЎЈ©
A. 1ёц B. 2ёц C. 3ёц D. 4ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїAЎўBБЅЦЦРНєЕµД»ъЖчјУ№¤Н¬Т»ЦЦБгјюЈ¬ТСЦЄAРН»ъЖч±ИBРН»ъЖчГїРЎК±¶ајУ№¤20ёцБгјюЈ¬AРН»ъЖчјУ№¤400ёцБгјюЛщУГК±јдУлBРН»ъЖчјУ№¤300ёцБгјюЛщУГК±јдПаН¬Ј®AРН»ъЖчГїРЎК±јУ№¤БгјюµДёцКэ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОOABCµД¶ҐµгAЈ¬C·Ц±рФЪЈшЦбєНЈщЦбЙПЈ¬µгBµДЧш±кОЄЈЁ2Ј¬3Ј©ЎЈЛ«ЗъПЯ![]() µДНјПсѕ№эBCµДЦРµгDЈ¬ЗТУлABЅ»УЪµгEЈ¬Б¬ЅУDEЎЈ
µДНјПсѕ№эBCµДЦРµгDЈ¬ЗТУлABЅ»УЪµгEЈ¬Б¬ЅУDEЎЈ

ЈЁ1Ј©ЗуkµДЦµј°µгEµДЧш±кЈ»
ЈЁ2Ј©ИфµгFКЗ±ЯЙПТ»µгЈ¬ЗТЎчFBCЎЧЎчDEBЈ¬ЗуЦ±ПЯFBµДЅвОцКЅ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄAЈ¬BКЗ·ґ±ИАэєЇКэy=![]() ЈЁkЈѕ0Ј¬xЈѕ0Ј©НјПуЙПµДБЅµгЈ¬BCЎОxЦбЈ¬Ѕ»yЦбУЪµгCЈ¬¶ЇµгPґУЧш±кФµгOіц·ўЈ¬СШOЎъAЎъBЎъCЈЁНјЦРЎ°ЎъЎ±ЛщКѕВ·ПЯЈ©ФИЛЩФЛ¶ЇЈ¬ЦХµгОЄCЈ¬№эPЧчPMЎНxЦбЈ¬ґ№ЧгОЄMЈ®ЙиИэЅЗРОOMPµДГж»эОЄSЈ¬PµгФЛ¶ЇК±јдОЄtЈ¬ФтS№ШУЪxµДєЇКэНјПуґуЦВОЄЈЁ Ј©
ЈЁkЈѕ0Ј¬xЈѕ0Ј©НјПуЙПµДБЅµгЈ¬BCЎОxЦбЈ¬Ѕ»yЦбУЪµгCЈ¬¶ЇµгPґУЧш±кФµгOіц·ўЈ¬СШOЎъAЎъBЎъCЈЁНјЦРЎ°ЎъЎ±ЛщКѕВ·ПЯЈ©ФИЛЩФЛ¶ЇЈ¬ЦХµгОЄCЈ¬№эPЧчPMЎНxЦбЈ¬ґ№ЧгОЄMЈ®ЙиИэЅЗРОOMPµДГж»эОЄSЈ¬PµгФЛ¶ЇК±јдОЄtЈ¬ФтS№ШУЪxµДєЇКэНјПуґуЦВОЄЈЁ Ј©

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ХэОе±ЯРОµД±Яі¤ОЄ2Ј¬Б¬ЅУ¶ФЅЗПЯADЈ¬BEЈ¬CEЈ¬ПЯ¶ОAD·Ц±рУлBEєНCEПаЅ»УЪµгMЈ¬NЈ¬ёшіцПВБРЅбВЫЈєўЩЎПAME=108ЎгЈ»ўЪ![]() Ј»ўЫMN=
Ј»ўЫMN=![]() Ј»ўЬ
Ј»ўЬ![]() Ј®ЖдЦРХэИ·ЅбВЫµДРтєЕКЗ_____Ј®
Ј®ЖдЦРХэИ·ЅбВЫµДРтєЕКЗ_____Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЧТТБЅµШПаѕа180kmЈ¬Т»БРВэіµТФ40km/hµДЛЩ¶ИґУјЧµШФИЛЩК»НщТТµШЈ¬Вэіµіц·ў30·ЦЦУєуЈ¬Т»БРїміµТФ60km/hµДЛЩ¶ИґУјЧµШФИЛЩК»НщТТµШЈ®БЅіµПајМµЅґпЦХµгТТµШЈ¬ФЩґО№эіМЦРЈ¬БЅіµЗЎєГПаѕа10kmµДґОКэКЗЈЁ Ј©
A.1B.2C.3D.4
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїС§РЈЧј±ё№єЅшТ»ЕъЅЪДЬµЖЈ¬ТСЦЄ1Ц»AРНЅЪДЬµЖєН3Ц»BРНЅЪДЬµЖ№ІРи26ФЄЈ»3Ц»AРНЅЪДЬµЖєН2Ц»BРНЅЪДЬµЖ№ІРи29ФЄЈ®
ЈЁ1Ј©ЗуТ»Ц»AРНЅЪДЬµЖєНТ»Ц»BРНЅЪДЬµЖµДКЫјЫёчКЗ¶аЙЩФЄЈ»
ЈЁ2Ј©С§РЈЧј±ё№єЅшХвБЅЦЦРНєЕµДЅЪДЬµЖ№І50Ц»Ј¬ІўЗТAРНЅЪДЬµЖµДКэБїІ»¶аУЪBРНЅЪДЬµЖКэБїµД3±¶Ј¬ЗлЙијЖіцЧоКЎЗ®µД№єВт·Ѕ°ёЈ¬ІўЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com