
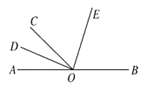
【题目】已知![]() 、
、![]() 、
、![]() 三点在同一条直线上,
三点在同一条直线上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)![]() 是否随
是否随![]() 的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
【答案】(1)90°;(2)90°;(3)∠DOE不随∠AOC的度数的变化而变化,∠DOE=90°,理由见解析.
【解析】
(1)由角平分线的定义求出∠COD的度数,在由平角和角平分线的定义求出∠COE,即可求出∠DOE;
(2)同(1)的方法可求出∠DOE;
(3)设∠AOC=![]() ,然后依照(1)的方法进行推导得出结论.
,然后依照(1)的方法进行推导得出结论.
解:(1)∵OD平分∠AOC,∠AOC=40°,
∴∠COD=![]() ∠AOC=20°,∠BOC=
∠AOC=20°,∠BOC=![]()
又∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=70°
∠BOC=70°
∴∠DOE=∠COD+∠COE=![]()
(2)∵OD平分∠AOC,∠AOC=60°,
∴∠COD=![]() ∠AOC=30°,∠BOC=
∠AOC=30°,∠BOC=![]()
又∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°
∠BOC=60°
∴∠DOE=∠COD+∠COE=![]()
(3)∠DOE不随∠AOC的度数的变化而变化,∠DOE=90°,理由如下:
设∠AOC=![]() ,
,
∵OD平分∠AOC,
∴∠COD=![]() ∠AOC=
∠AOC=![]() ,∠BOC=
,∠BOC=![]()
又∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=
∠BOC=![]()
∴∠DOE=∠COD+∠COE=![]()
故∠DOE不随∠AOC的度数的变化而变化,始终等于90°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①有理数包括正有理数和负有理数; ②绝对值等于它本身的数是非负数;③若|b|=|﹣5|,则b=-5 ; ④当b=2时,5﹣|2b﹣4|有最小值是5;⑤若![]() 、
、![]() 互为相反数,则
互为相反数,则![]() ;⑥
;⑥![]() 是关于
是关于![]() 、
、![]() 的六次三项式.
的六次三项式.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:①∠AME=108°;②![]() ;③MN=
;③MN=![]() ;④
;④![]() .其中正确结论的序号是_____.
.其中正确结论的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆![]() 中,
中,![]() 、
、![]() 是圆
是圆![]() 的半径,点
的半径,点![]() 在劣弧弧
在劣弧弧![]() 上,
上,![]() ,
,![]() ,
,![]() ∥
∥![]() ,联结
,联结![]() .
.
(1)如图1,求证:![]() 平分
平分![]() ;
;
(2)点![]() 在弦
在弦![]() 的延长线上,联结
的延长线上,联结![]() ,如果△
,如果△![]() 是直角三角形,请你在如图2中画出
是直角三角形,请你在如图2中画出
点![]() 的位置并求
的位置并求![]() 的长;
的长;
(3)如图3,点![]() 在弦
在弦![]() 上,与点
上,与点![]() 不重合,联结
不重合,联结![]() 与弦
与弦![]() 交于点
交于点![]() ,设点
,设点![]() 与点
与点![]() 的
的
距离为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次趣味数学党赛,满分100分,学生得分均为整数,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100
乙组:50,60,60,60,70,70,70,70,80,90.
组别 | 平均分 | 中位数 | 方差 |
甲组 | 68 | a | 376 |
乙组 | b | 70 |
(1)以生成绩统计分析表中a=_________分,b=_________分.
(2)小亮同学说:“这次赛我得了70分,在我们小组中属中游略偏上!”双察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由。
(3)计算乙组成的方差,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会进择哪一组?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=![]() BC,求线段PQ的长.
BC,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com