
【题目】北国超市销售每台进价分别为400元、350元的![]() 两种型号的豆浆机.下表是近两周的销售情况:
两种型号的豆浆机.下表是近两周的销售情况:
销售数量:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 5台 | 3500元 |
第二周 | 4台 | 10台 | 6000元 |
(进价、售价均保持不变,利润=销售收入-进价)
(1)求![]() 两种型号的豆浆机的销售单价;
两种型号的豆浆机的销售单价;
(2 )若第三周该超市采购这两种型号的豆浆机共20台, 并且B型号的台数比A型号的台数的2倍少1 ,如果这20台豆浆机全部售出,求这周销售的利润;
(3)若恰好用8000元采购这两种型号的豆浆机,问有哪几种进货方案? ( 要求两种型号都要采购)
【答案】(1) ![]() 型豆浆机的销售单价为500元/台,
型豆浆机的销售单价为500元/台,![]() 型豆浆机的单价为400元/台;(2) 1350元 ;(3)有两种进货方案:方案一:
型豆浆机的单价为400元/台;(2) 1350元 ;(3)有两种进货方案:方案一: ![]() 型号豆浆机13台,
型号豆浆机13台, ![]() 型号豆浆机8台;方案二:
型号豆浆机8台;方案二:![]() 型号豆浆机6台,
型号豆浆机6台, ![]() 型号豆浆机16台.
型号豆浆机16台.
【解析】
(1) 设![]() 两种型号的豆浆机的销售单价分别为x元、y元,根据题意列方程组求解即可;
两种型号的豆浆机的销售单价分别为x元、y元,根据题意列方程组求解即可;
(2) 设采购A两种型号的豆浆机a台,则采购B两种型号的豆浆机 (20a)台,求出a的值再求这周销售的利润即可;
(3) 设采购![]() 两种型号的豆浆机分别为m台、n台,400m+350n=8000,再根据m、n均为自然数讨论即可得到方案.
两种型号的豆浆机分别为m台、n台,400m+350n=8000,再根据m、n均为自然数讨论即可得到方案.
解:(1) 设![]() 两种型号的豆浆机的销售单价分别为x元、y元,
两种型号的豆浆机的销售单价分别为x元、y元,
依题意得:![]() ,
,
解得:![]() ,
,
答:![]() 两种型号的豆浆机的销售单价分别为500元、400元;
两种型号的豆浆机的销售单价分别为500元、400元;
(2)设采购A两种型号的豆浆机a台,则采购B两种型号的豆浆机 (20a)台.
依题意得:20-a=2a-1,
解得:a=7.
∴采购A两种型号的豆浆机7台,采购B两种型号的豆浆机13台,
∴这周销售的利润=7×(500-400)+13×(400-350)=700+650=1350(元)
答:这周销售的利润1350元;
(3) 设采购![]() 两种型号的豆浆机分别为m台、n台,依题意得,
两种型号的豆浆机分别为m台、n台,依题意得,
400m+350n=8000, 其中m、n均为自然数.
于是有:![]() ,
,
∴当n=8时,m=13;
当n=16时,m=6.
答:有两种进货方案:
方案一: ![]() 型号豆浆机13台,
型号豆浆机13台, ![]() 型号豆浆机8台;
型号豆浆机8台;
方案二:![]() 型号豆浆机6台,
型号豆浆机6台, ![]() 型号豆浆机16台..
型号豆浆机16台..


科目:初中数学 来源: 题型:
【题目】如图已知∠1与线段a,用直尺和圆规按下列步骤作图(保留作图痕迹,不写做法。)
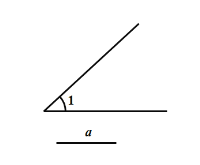
(1)作等∠A于∠1
(2)在∠A的两边分别作AM=AN=a
(3)连接MN
查看答案和解析>>
科目:初中数学 来源: 题型:
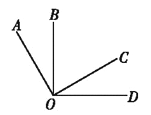
【题目】如图,两个直角![]() 和
和![]() 有公共顶点
有公共顶点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③若
;③若![]() 平分
平分![]() ,则
,则![]() 平分
平分![]() ;④
;④![]() 的平分线与
的平分线与![]() 的平分线是同一条射线.其中结论正确的个数是( )
的平分线是同一条射线.其中结论正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
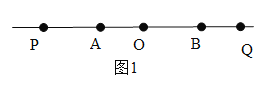
【题目】如图①,直线![]() 上依次有
上依次有![]() 、
、![]() 、
、![]() 三点,若射线
三点,若射线![]() 绕点
绕点![]() 沿顺时针方向以每秒
沿顺时针方向以每秒![]() 的速度旋转,同时射线
的速度旋转,同时射线![]() 绕点
绕点![]() 沿逆时针方向以每秒
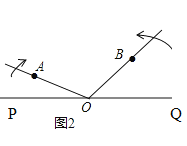
沿逆时针方向以每秒![]() 的速度旋转,如图②,设旋转时间为
的速度旋转,如图②,设旋转时间为![]() 秒(
秒(![]() ).
).
(1)![]() __________度,
__________度,![]() __________度.(用含
__________度.(用含![]() 的代数式表示)
的代数式表示)
(2)在运动过程中,当![]() 等于
等于![]() 时,求
时,求![]() 的值.
的值.
(3)在旋转过程中是否存在这样的![]() ,使得射线
,使得射线![]() 平分
平分![]() 或
或![]() (
(![]() ,
,![]() 均为小于
均为小于![]() 的角)?如果存在,直接写出
的角)?如果存在,直接写出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
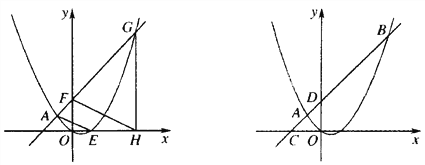
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
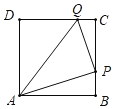
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
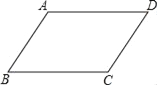
【题目】如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com