
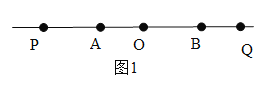
【题目】如图①,直线![]() 上依次有
上依次有![]() 、
、![]() 、
、![]() 三点,若射线
三点,若射线![]() 绕点
绕点![]() 沿顺时针方向以每秒
沿顺时针方向以每秒![]() 的速度旋转,同时射线
的速度旋转,同时射线![]() 绕点
绕点![]() 沿逆时针方向以每秒
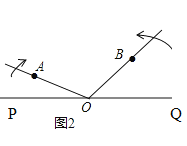
沿逆时针方向以每秒![]() 的速度旋转,如图②,设旋转时间为
的速度旋转,如图②,设旋转时间为![]() 秒(
秒(![]() ).
).
(1)![]() __________度,
__________度,![]() __________度.(用含
__________度.(用含![]() 的代数式表示)
的代数式表示)
(2)在运动过程中,当![]() 等于
等于![]() 时,求
时,求![]() 的值.
的值.
(3)在旋转过程中是否存在这样的![]() ,使得射线
,使得射线![]() 平分
平分![]() 或
或![]() (
(![]() ,
,![]() 均为小于
均为小于![]() 的角)?如果存在,直接写出
的角)?如果存在,直接写出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)![]() 度,
度,![]() 度;(2)当
度;(2)当![]() 等于
等于![]() 时,t=20或40;(3)射线
时,t=20或40;(3)射线![]() 平分
平分![]() 或
或![]() 时,t=18或36.
时,t=18或36.
【解析】
(1)∠POA的度数等于OA旋转速度乘以旋转时间,∠QOB的度数等于OB旋转速度乘以旋转时间;
(2)分OA与OB相遇前,∠AOB=60°,和OA与OB相遇后,∠AOB=60°,两种情况,列出关于t的等式,解出即可;
(3)分OB平分∠AOQ和OB平分∠AOP两种情况,列出关于t的等式,解出即可.
(1)![]() 度,
度,
![]() 度;
度;
(2)①OA与OB相遇前,∠AOB=60°,
![]()
![]()
![]() ;
;
②OA与OB相遇后,∠AOB=60°,
![]()
![]()
![]() ,
,
综上,当![]() 等于
等于![]() 时,t=20或40;
时,t=20或40;
(3)①OB平分∠AOQ时,
∠AOQ=2∠BOQ,
![]()
![]()
![]() ;
;
②OB平分∠AOP时,
∠AOP=2∠BOP,
![]()
![]()
![]()
![]() ,
,
综上,射线![]() 平分
平分![]() 或
或![]() 时,t=18或36.
时,t=18或36.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
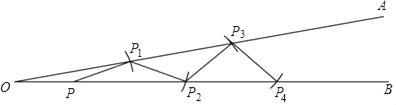
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系中,点![]() 、点
、点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,另有两点
,另有两点![]() 和
和![]() ,
,![]() 、
、![]() 均大于
均大于![]() ;
;
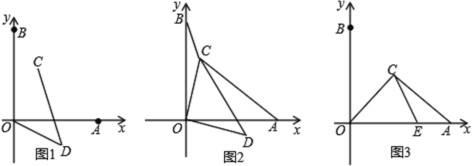
(1)连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北国超市销售每台进价分别为400元、350元的![]() 两种型号的豆浆机.下表是近两周的销售情况:
两种型号的豆浆机.下表是近两周的销售情况:
销售数量:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 5台 | 3500元 |
第二周 | 4台 | 10台 | 6000元 |
(进价、售价均保持不变,利润=销售收入-进价)
(1)求![]() 两种型号的豆浆机的销售单价;
两种型号的豆浆机的销售单价;
(2 )若第三周该超市采购这两种型号的豆浆机共20台, 并且B型号的台数比A型号的台数的2倍少1 ,如果这20台豆浆机全部售出,求这周销售的利润;
(3)若恰好用8000元采购这两种型号的豆浆机,问有哪几种进货方案? ( 要求两种型号都要采购)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() .
.
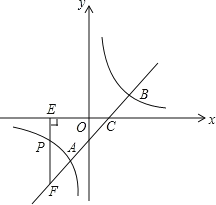
(1)求反比例函数的解析式;
(2)若点![]() 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
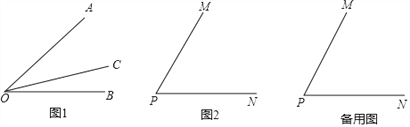
【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com