Question

4．如图，⊙O的半径为2，点O到直线l的距离为4，过l上任一点P作⊙O的切线，切点为Q；若以PQ为边作正方形PQRS，则正方形PQRS的面积最小值为12．

Answer 1

分析 连接OQ、OP，如图，根据切线的性质得OQ⊥PQ，则利用勾股定理得到PQ²=OP²-OQ²=OP²-4，也是判断OP取最小值时，PQ²的值最小，此时正方形PQRS的面积有最小值，根据垂线段最短得到OP的最小值为4，于是得到PQ²的最小值，从而确定正方形PQRS的面积的最小值．

解答 解：连接OQ、OP，如图，
∵PQ为切线，
∴OQ⊥PQ，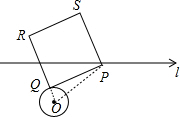
在Rt△OPQ中，PQ²=OP²-OQ²=OP²-4，
当OP取最小值时，PQ²的值最小，此时正方形PQRS的面积有最小值，
而当OP⊥l时，OP取最小值，
∴OP的最小值为4，
∴PQ²的最小值为16-4=12，
∴正方形PQRS的面积最小值为12．
故答案为12．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．充分利用垂线段最短解决最小值问题．