Question

已知点O是直线AB上的一点，∠COE=90°，OF是∠AOE的平分线．

（1）当∠AOC=40°，点C、E、F在直线AB的同侧（如图1所示）时，求∠BOE和∠COF的度数．
（2）当∠AOC=40°，点C与点E、F在直线AB的两旁（如图2所示）时，求∠BOE和∠COF的度数．
（3）当∠AOC=n°，请选择图（1）或图（2）一种情况计算，
∠BOE=______
∠COF=______（用含n的式子表示）
（4）根据以上计算猜想∠BOE与∠COF的数量关系______（直接写出结果）．

Answer 1

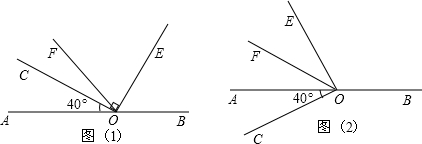
解：（1）如图（1），
∵∠AOC=40°，∠COE是直角，
∴∠AOE=130°，
∴∠BOE=180°-130°=50°，
又∵OF平分∠AOE，
∴∠AOF=∠AOE=65°，
∴∠COF=65°-40°=25°；

（2）如图（2），
∵∠AOC=40°，∠COE是直角，
∴∠AOE=50°，
∴∠BOE=180°-50°=130°，
又∵OF平分∠AOE，
∴∠AOF=∠AOE=25°，
∴∠COF=25°+40°=65°；

（3）如图（2），
∵∠AOC=n°，∠COE是直角，
∴∠AOE=（90-n）°，
∴∠BOE=180°-（90-n）°=（90+n）°，
又∵OF平分∠AOE，
∴∠AOF=∠AOE=（45-n）°，
∴∠COF=n°+（45-n）°=45°n°；
故答案为：（90+n）°，45°n°；

（4）根据以上计算的∠BOE和∠COF的度数可得：
∠BOE=2∠COF．
故答案为：∠BOE=2∠COF．
分析：（1）根据∠AOC=40°，∠COE是直角，即可得出∠AOE的度数以及∠BOE的度数，再利用角平分线的性质得出∠AOF的度数，进而得出答案；
（2）根据∠AOC=40°，∠COE是直角，得出∠AOE的度数，再利用角平分线的性质得出∠AOF的度数，进而得出答案；
（3）根据（2）中所的方法即可得出∠BOE以及∠COF的度数，进而得出答案；
（4）根据以上所求即可得出∠BOE与∠COF的数量关系．
点评：此题主要考查了角的计算以及角平分线的性质，根据数形结合以及角平分线的性质得出是解题关键．