
 ��ͼ��������y=-$\frac{1}{2}$x2+bx+c��ͼ���A��0��1����B��1��3�����㣬��ABΪ����������ABCD����D��x���ϣ����ӳ�BC��x���ڵ�E��
��ͼ��������y=-$\frac{1}{2}$x2+bx+c��ͼ���A��0��1����B��1��3�����㣬��ABΪ����������ABCD����D��x���ϣ����ӳ�BC��x���ڵ�E������ ��1�����ô���ϵ��������κ����Ľ���ʽ��
��2����ͼ1���������ߣ�����ȫ�������Σ�֤����GAB�ա�ODA��HL������OD=AG=2����D��2��0��������ͬ�ǵ����Ǻ���sin��ADO=sin��DEC�б���ʽ�����DE�ij�������OE�ij���д��E�����ꣻ
��3����ͼ2�������ô���ϵ������ֱ��BC�Ľ���ʽ����������������ֱ��BC�������ߵĽ���F�����꣬�����߶�MH�����㵱t=3ʱPQ�ij���HN�ij������������
�ڵ�P��Q�ĺ����궼��7-t���ֱ������������ʽ���������ꣻ
�����������
i����0��t��2ʱ����ͼ3��M�ڱ�AD�ϣ�
ii����2��t��4ʱ����ͼ4��M�ڱ�CD�ϣ�
iii����4��t��6ʱ����ͼ5��M�ڱ�BC�ϣ�
ǰ����������ֱ����PQ��HN�ij������������ʽ��������ɣ�������������������ߣ������M�ĺ����꣬����M��ֱ��PQ�ϣ�������������һ��ֱ���ϣ����Ϊ0��
��� �⣺��1����������y=-$\frac{1}{2}$x2+bx+c��ͼ���A��0��1����B��1��3����
��$\left\{\begin{array}{l}{c=1}\\{-\frac{1}{2}+b+c=3}\end{array}\right.$�����$\left\{\begin{array}{l}c=1\\ b=\frac{5}{2}\end{array}$��
�������ߵı���ʽΪ��y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+1��
��2����ͼ1������B��BG��y���ڵ�G��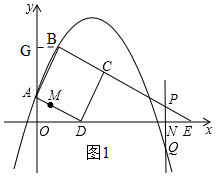
��B��1��3����
��GB=1��OG=3��
��A��0��1����
��OA=1��GB=OA��
��AG=OG-OA=3-1=2��
���ı���ABCD�������Σ�
��AB=AD��
�ߡ�BGA=��AOD=90�㣬GB=OA��
���GAB�ա�ODA��HL����
��OD=AG=2��
��D��2��0����
��CD=AD=$\sqrt{AO^2+OD^2}$=$\sqrt{1^2+2^2}$=$\sqrt{5}$��
���ı���ABCD�������Σ�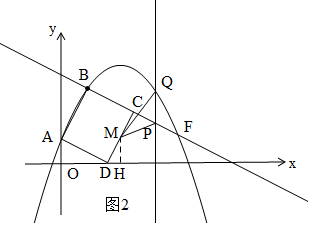
��AD��BC��
���ADO=��DEC��
��sin��ADO=sin��DEC����$\frac{AO}{AD}$=$\frac{CD}{DE}$��$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{DE}$��
��DE=5��
��OE=OD+DE=2+5=7��
��E��7��0����
��3����ͼ2������ֱ��BC��y=mx+n��
��ֱ��BC��y=mx+n��B��1��3����E��7��0�����㣬
��$\left\{\begin{array}{l}m+n=3\\ 7m+n=0\end{array}$�����$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=\frac{7}{2}}\end{array}\right.$��
��ֱ��BC��y=-$\frac{1}{2}$x+$\frac{7}{2}$��
��ֱ��BC�������߽���B��F���㣬
����$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{5}{2}x+1}\\{y=-\frac{1}{2}x+\frac{7}{2}}\end{array}\right.$�����F��5��1����
��t=3ʱ����M�˶���·��Ϊ��$\frac{\sqrt{5}}{2}$��3=AD+DM=$\sqrt{5}$+DM��
��DM=$\frac{\sqrt{5}}{2}$��
��N�˶���·��Ϊ��NE=3��ON=4��
��xF=5��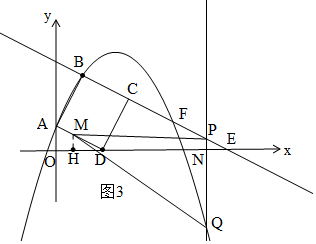
���N��F����࣮
����M��MH��OE�ڵ�H��
��DH=DM•cos��MDH=$\frac{\sqrt{5}}{2}$��$\frac{1}{\sqrt{5}}$=$\frac{1}{2}$��
��HN=ON-OD-DH=4-2-$\frac{1}{2}$=$\frac{3}{2}$��
��xQ=4ʱ��yQ=3����xP=4ʱ��yP=$\frac{3}{2}$��
��PQ=yQ-yP=3-$\frac{3}{2}$=$\frac{3}{2}$��
��S��MPQ=$\frac{1}{2}$PQ•HN=$\frac{1}{2}$��$\frac{3}{2}$��$\frac{3}{2}$=$\frac{9}{8}$��
��������ã�P��7-t��$\frac{1}{2}$t����Q��7-t��-$\frac{1}{2}{t}^{2}$+$\frac{9}{2}t$-6��
i����0��t��2ʱ����ͼ3��M�ڱ�AD�ϣ�PQ=$\frac{1}{2}$t-��-$\frac{1}{2}{t}^{2}$+$\frac{9}{2}t$-6��=$\frac{1}{2}{t}^{2}$-4t+6��
AM=$\frac{\sqrt{5}}{2}t$��DM=$\sqrt{5}$-$\frac{\sqrt{5}}{2}$t��
cos��ODM=$\frac{DH}{DM}=\frac{2}{\sqrt{5}}$��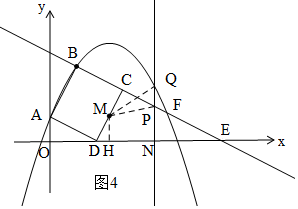
��DH=DM•cos��ODM=��$\sqrt{5}$-$\frac{\sqrt{5}}{2}$t����$\frac{2}{\sqrt{5}}$=2-t��
��OH=2-DH=2-��2-t��=t��
��HN=OE-OH-EN=7-t-t=7-2t��
S��MPQ=$\frac{1}{2}$PQ•HN=$\frac{1}{2}$��$\frac{1}{2}{t}^{2}$-4t+6����7-2t��=-$\frac{1}{4}$��2t-7����t2-8t+12����
ii����2��t��4ʱ����ͼ4��M�ڱ�CD�ϣ�
PQ=-$\frac{1}{2}{t}^{2}$+$\frac{9}{2}t$-6-��$\frac{1}{2}t$��=-$\frac{1}{2}{t}^{2}$+4t-6��
DH=DM•cos��HDM=��$\frac{\sqrt{5}}{2}t$-$\sqrt{5}$����$\frac{1}{\sqrt{5}}$=$\frac{1}{2}t$-1��
HN=ON-OD-DH=7-t-2-��$\frac{1}{2}$t-1��=6-$\frac{3}{2}$t��
S��MPQ=$\frac{1}{2}$PQ•HN=$\frac{1}{2}$��-$\frac{1}{2}{t}^{2}$+4t-6����6-$\frac{3}{2}$t��=$\frac{3}{8}$��t-4����t2-8t+12����
iii����4��t��6ʱ����ͼ5��M�ڱ�BC�ϣ�
��M��MH��y����H����CM=$\frac{\sqrt{5}}{2}t-2\sqrt{5}$��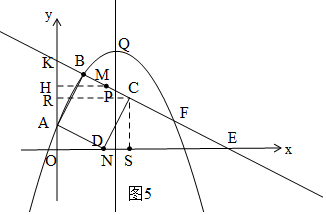
��C��CS��x����S��
��֤����AOD�ա�DSC��
��DS=OA=1��SC=OD=2��
��C��3��2����
��C��CR��y����R��
��CR=OS=3��KR=OK-OR=$\frac{7}{2}$-2=$\frac{3}{2}$��
�ɹ��ɶ����ã�KC=$\sqrt{��\frac{3}{2}��^{2}+{3}^{2}}$=$\frac{3\sqrt{5}}{2}$��KE=$\sqrt{{7}^{2}+��\frac{7}{2}��^{2}}$=$\frac{7\sqrt{5}}{2}$��
��KM=KC-CM=$\frac{3\sqrt{5}}{2}$-��$\frac{\sqrt{5}}{2}t-2\sqrt{5}$��=-$\frac{\sqrt{5}}{2}$t+$\frac{7\sqrt{5}}{2}$��
cos��KMH=cos��KEO=$\frac{7}{\frac{7\sqrt{5}}{2}}$=$\frac{HM}{-\frac{\sqrt{5}t}{2}+\frac{7\sqrt{5}}{2}}$��
��HM=7-t��
����M��ֱ��PQ�ϣ�
��ʱ��S��MPQ=0��
����������S��MPQ=$\left\{\begin{array}{l}{-\frac{1}{4}��2t-7����{t}^{2}-8t+12����0��t��2��}\\{\frac{3}{8}��t-4����{t}^{2}-8t+12����2��t��4��}\\{0��4��t��6��}\end{array}\right.$��
���� �����Ƕ��κ������ۺ��⣬���������ô���ϵ��������κ�����һ�κ����Ľ���ʽ�������ε����ʡ�������ȫ�ȵ����ʺ��ж���ͼ���������ص��Լ���������������ڵ������У������������������ʾ�߶εij��ǹؼ���ͬʱ�������ν�ϵ�˼�룬��ȷ������˶�·�̣���������������۵ó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 5 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
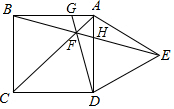 ��ͼ����������ABCD��������ȱߡ�ADE������BE��AC�ڵ�F����AD�ڵ�H������DF���ӳ���AB�ڵ�G�����н����У���ȷ�ĸ����ǣ�������
��ͼ����������ABCD��������ȱߡ�ADE������BE��AC�ڵ�F����AD�ڵ�H������DF���ӳ���AB�ڵ�G�����н����У���ȷ�ĸ����ǣ�������| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
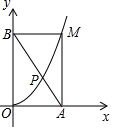 ��ͼ����M��������y=ax2��x��0���ϵ�����һ�㣬MA��x���ڵ�A��MB��y���ڵ�B������AB�����������ڵ�P����$\frac{PA}{PB}$��ֵ�ǣ�������
��ͼ����M��������y=ax2��x��0���ϵ�����һ�㣬MA��x���ڵ�A��MB��y���ڵ�B������AB�����������ڵ�P����$\frac{PA}{PB}$��ֵ�ǣ�������| A�� | $\frac{\sqrt{5}-1}{2}$ | B�� | $\frac{\sqrt{5}+1}{2}$ | C�� | $\frac{3-\sqrt{5}}{2}$ | D�� | $\frac{3+\sqrt{5}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AD=$\sqrt{2}$AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ�
��ͼ���ھ���ABCD�У�AD=$\sqrt{2}$AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ�| A�� | �٢ڢۢܢ� | B�� | �٢ڢۢ� | C�� | �٢ۢܢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com