
【题目】(1)特例探究.
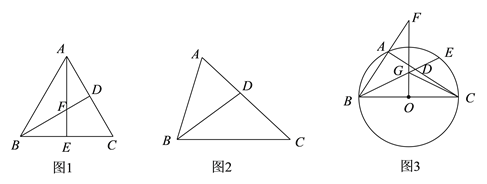
如图(1),在等边三角形ABC中,BD是∠ABC的平分线,AE是BC边上的高线,BD和AE相交于点F.
请你探究![]() 是否成立,请说明理由;请你探究
是否成立,请说明理由;请你探究![]() 是否成立,并说明理由.
是否成立,并说明理由.
(2)归纳证明.
如图(2),若△ABC为任意三角形,BD是三角形的一条内角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)拓展应用.
如图(3),BC是△ABC外接圆⊙O的直径,BD是∠ABC的平分线,交⊙O于点E,过点O作BC的垂线,交BA的延长线于点F,交BD于点G,连接CG,其中cos∠ACB=![]() ,请直接写出
,请直接写出![]() 的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
【答案】(1)成立,证明见解析;(2)成立,证明见解析;(3)![]() S.
S.
【解析】
(1)由等边三角形的性质结合已知条件易得:AD=CD,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,由此可得AF=BF=2EF,从而可得![]() ,
,![]() ;
;
(2)如下图,过点D作DE⊥AB于点E,DF⊥BC于点F,过点B作BP⊥AC于点P,则易得DE=DF,由此可得S△ABD=![]() AB·DE=
AB·DE=![]() AD·BP,S△CBD=
AD·BP,S△CBD=![]() BC·DF=
BC·DF=![]() CD·BP,把两个等式相比即可得到所求结论了;
CD·BP,把两个等式相比即可得到所求结论了;
(3)①由BC是⊙O的直径可得∠BAC=90°,结合cos∠ACB=![]() 可得sin∠ACB=
可得sin∠ACB=![]() ,再由(2)中结论即可得到
,再由(2)中结论即可得到![]() ;②由已知条件易得
;②由已知条件易得![]() ,由OF⊥BC可得
,由OF⊥BC可得![]() ,从而可得
,从而可得![]() ,由此即可得到S△COG=
,由此即可得到S△COG=![]() .
.
(1)![]() ,
,![]() ,理由如下:
,理由如下:
∵△ABC为等边三角形,BD是∠ABC的平分线,AE是BC边上的高线,
∴AD=CD=![]() AC,BE=
AC,BE=![]() BC ,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,
BC ,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,
∴AF=BF=2EF,
∴![]() ,
,![]() ;
;
(2)![]() 一定成立,理由如下:
一定成立,理由如下:
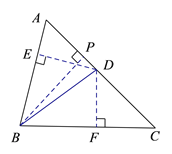
如下图,过点D作DE⊥AB于点E,DF⊥BC于点F,过点B作BP⊥AC于点P,
∵BD是∠ABC的平分线,
∴DE=DF,
∵S△ABD=![]() AB·DE=
AB·DE=![]() AD·BP,S△CBD=
AD·BP,S△CBD=![]() BC·DF=
BC·DF=![]() CD·BP,
CD·BP,
∴![]()
∴![]() .
.
(3)∵BC为直径,
∴∠BAC=90°.
在Rt△ABC中,∠BAC=90°,cos∠ACB=![]() ,
,
∴sin∠ACB=![]() .
.
∵BD是∠ABC的平分线,
∴![]() .
.
∵点G在∠ABC的平分线上,
∴△BGF和△COG等高(分别以BF、CO为底),
∴![]() .
.
∵FO⊥BC,
∴![]() =cos∠ABC=sin∠ACB=
=cos∠ABC=sin∠ACB=![]() ,
,
又∵S△BGF=S,
∴![]() ,
,
∴S△COG=![]() S.
S.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).

A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
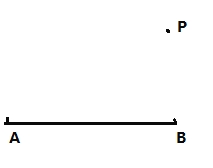
【题目】如图,已知线段![]() 和线段
和线段![]() 外的一点
外的一点![]() ,请按下列要求画出相应的图形,并计算(不要求写画法):
,请按下列要求画出相应的图形,并计算(不要求写画法):
(1)①延长线段![]() 到
到![]() ,使
,使![]() ;
;
②若![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求线段
,求线段![]() 的长.
的长.
(2)过点![]() 画
画![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() 并用直尺测量线段
并用直尺测量线段![]() 、
、![]() 、
、![]() 的长,并指出哪条线段可以表示点
的长,并指出哪条线段可以表示点![]() 到线段
到线段![]() 的距离.(测量数据直接标注在图形上,结果精确到
的距离.(测量数据直接标注在图形上,结果精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
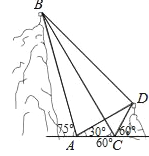
【题目】如图,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°.于水面C处测得B点和D点的仰角均为60°,AC=0.1km.
(1)试探究图中B,D间距离与另外哪两点间距离相等;
(2)求B点距水平面的高度(计算结果精确到0.01km,参考数据:![]() ≈1.73,tan75°≈3.73)
≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=
BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=![]() BC.其中成立的有( )
BC.其中成立的有( )

A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
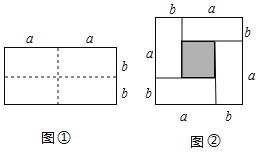
【题目】(1)如图①是一个长为2a,宽为2b的长方形,若将此图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的什么量不变?请填写这个量的名称 .所得的正方形的面积比原长方形的面积多出的阴影部分的面积用含a,b的代数式表示 ;
(2)由①的探索中,可以得出的结论是:在周长一定的长方形中,当 时,面积最大;
(3)若一长方形的周长为36厘米,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年是中国工农红军长征胜利80周年,某商家用1200元购进了一批长征胜利主题纪念衫,上市后果然供不应求,商家又用2800元购进了第二批这种纪念衫,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批纪念衫单价是多少元?
(2)若两批纪念衫按相同的标价销售,最后剩下20件按标价八折优惠卖出,如果两批纪念衫全部售完利润不低于640元(不考虑其它因素),那么每件纪念衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com