
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°. 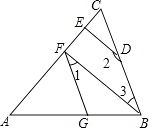
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
【答案】
(1)解:(1)BF∥DE,理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)解:∵BF∥DE,BF⊥AC,
∴DE⊥AC,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∴∠AFG=90°﹣30°=60°.
【解析】(1)由于∠AGF=∠ABC,可判断GF∥BC,则∠1=∠3,由∠1+∠2=180°得出∠3+∠2=180°判断出BF∥DE;(2)由BF∥DE,BF⊥AC得到DE⊥AC,由∠2=150°得出∠1=30°,得出∠AFG的度数
【考点精析】利用余角和补角的特征和垂线的性质对题目进行判断即可得到答案,需要熟知互余、互补是指两个角的数量关系,与两个角的位置无关;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 有理数包括整数和分数;
B. 一个代数式不是单项式就是多项式;
C. 几个有理数相乘,若负因数的个数是偶数个,则积为正数;
D. 绝对值等于它本身的数是0、1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )

A.①③⑤ B.②③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y cm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=![]() t2;
t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=![]() 秒,
秒,
其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
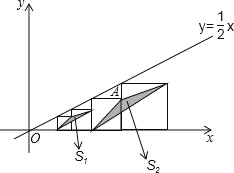
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=![]() x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是______,Sn的值为______.
x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是______,Sn的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,…通过观察,用你所发现的规律确定22009的个位数字是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)中日钓鱼岛争端持续,我海监船加大钓鱼岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.

(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com