练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，下列各图形各围绕哪一点，最低需要旋转多少度之后，能够与它的自身相重合？

    答案：
    解析：

    　　解　（1）180°；（2）；（3）（旋转中心这里就不再画了）．


    提示：

    　　分析　这类题首先要观察它是不是旋转对称图形，肯定之后再看它是由多少个相同的“单位”组成的，例如有n个．那么为使图形重合旋转的最低角度就是


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料，然后解答问题．
    经过正四边形（即正方形）各顶点的圆叫作这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫作这个圆的内接正四边形．
    如图，已知正四边形ABCD的外接圆⊙O，⊙O的面积为S1，正四边形ABCD的面积为S2，以圆心O为顶点作∠MON，使∠MON=90°，将∠MON绕点O旋转，OM、ON分别与⊙O相交于点E、F，分别与正四边形ABCD的边相交于点G、H．设由OE、OF、
    		EF
    及正四边形ABCD的边围成的图形（图中的阴影部分）的面积为S．①精英家教网
    （1）当OM经过点A时（如图①），则S、S1、S2之间的关系为：S=
     
    （用含S1、S2的代数式表示）；
    （2）当OM⊥AB时（如图②），点G为垂足，则（1）中的结论仍然成立吗？请说明理由；
    （3）当∠MON旋转到任意位置时（如图③），则（1）中的结论仍然成立吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在如图的平面直角坐标系中，请完成下列各题：
    （1）写出图中A，B，C，D各点的坐标；
    （2）描出E（1，0），F（-1，3），G（-3，0），H（-1，-3）；
    （3）顺次连接A，B，C，D各点，再顺次连接E，F，G，H，围成的两个封闭图形分别是什么图形？

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　北师大八年级版　2009－2010学年　第12期　总第168期 北师大版 题型：044

    在如图所示的平面直角坐标系中，请完成下列各题：

    (1)写出图中A，B，C，D各点坐标；

    (2)描出E(1，0)，F(－1，3)，G(－3，0)，H(－1，－3)；

    (3)顺次连接A、B、C、D各点，再顺次连接E、F、G、H，围成的两个封闭图形分别是什么图形？

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：探究题

    如图所示，将一些围棋子按照①②③④的方法摆放下去，第n个图形中的围棋子的总数目为s，解答下列问题：
    （1）按要求填表：
    （2）当n=10时，s=______；
    （3）根据上表中的数据把s作为点的纵坐标，n作为点的横坐标，在平面直角坐标系中描出相应的点；
    （4）请你猜一猜上述各点会在某函数图象上吗？如果在某一函数的图象上，请你求出s与n之间的关系．

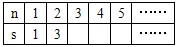
    查看答案和解析>>

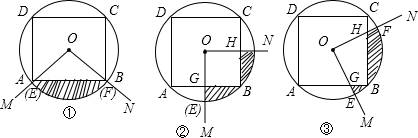
    科目：初中数学 来源：第3章《圆》中考题集（74）：3.7 弧长及扇形的面积（解析版） 题型：解答题

    阅读下列材料，然后解答问题．
    经过正四边形（即正方形）各顶点的圆叫作这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫作这个圆的内接正四边形．
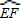    如图，已知正四边形ABCD的外接圆⊙O，⊙O的面积为S1，正四边形ABCD的面积为S2，以圆心O为顶点作∠MON，使∠MON=90°，将∠MON绕点O旋转，OM、ON分别与⊙O相交于点E、F，分别与正四边形ABCD的边相交于点G、H．设由OE、OF、及正四边形ABCD的边围成的图形（图中的阴影部分）的面积为S．①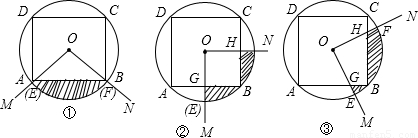
    （1）当OM经过点A时（如图①），则S、S1、S2之间的关系为：S=______（用含S1、S2的代数式表示）；
    （2）当OM⊥AB时（如图②），点G为垂足，则（1）中的结论仍然成立吗？请说明理由；
    （3）当∠MON旋转到任意位置时（如图③），则（1）中的结论仍然成立吗？请说明理由．

    查看答案和解析>>

    同步练习册答案