
����Ŀ����ͼ1��A��B��C��֣���ж���������������ŵ㣬��B��C�ֱ�λ�ڵ�A����������������AC=40�ף���λ�������˷ֱ��õ�BC�������±���
�� | �� | �� | �� | �� | �� | �� | �� | |
BC����λ���ף� | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
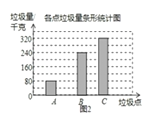
�����ֵ����˸�������������������������в�������ͳ��ͼ2��ͼ3��
��1�����е���λ����������������������
��2�������BC���ȵ�ƽ����![]() ��
��
��3����A����������������ͼ2����������
��4���ã�2���е�![]() ��ΪBC�ij��ȣ�Ҫ��A���������ص�·AB���˵�B������֪����1ǧ������ÿ�ķ���Ϊ0.005Ԫ��������������ķ��ã�
��ΪBC�ij��ȣ�Ҫ��A���������ص�·AB���˵�B������֪����1ǧ������ÿ�ķ���Ϊ0.005Ԫ��������������ķ��ã�
���𰸡���1��81�ף�84�ף���2��80�ף���3��80ǧ�ˣ���ͼ����������4��16![]() Ԫ
Ԫ
��������
��1��������λ���������Ķ���ֱ����⼴�ɣ�
��2������ƽ���������ó��𰸣�
��3������C�����������������ռ�İٷֱ��������������������������A��������ռ�İٷֱȼ������A�����������Ӷ���ȫͳ��ͼ��
��4������������Ǻ����ó�AB�ij��������ó�����������ķ��ã�
�⣺��1������Щ����С��������Ϊ��70��76��78��80��82��84��84��86��
����λ���ǣ�![]() ��81�ף�
��81�ף�
��84������2�Σ����ֵĴ�����࣬
��������84�ף�
�ʴ�Ϊ��81�ף�84�ף�
��2������BC���ȵ�ƽ�����ǣ�
![]() (��)��
(��)��
��3�����������ǣ�320��50%��640(ǧ��)��
��A�����������ǣ�640��(1��50%��37.5%)��80(ǧ��)��
��ȫ����ͼ��ͼ��
��4���ߵ�Bλ�ڵ�A����������
���BAC��90�㣬
��ֱ����ABC�У�
AB��![]() ��
��![]() ��40
��40![]() ��
��
������1ǧ������ÿ�ķ���Ϊ0.005Ԫ��
������������ķ���Ϊ��40![]() ��80��0.005��16
��80��0.005��16![]() (Ԫ)��
(Ԫ)��
������������ķ���Ϊ16![]() Ԫ��
Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
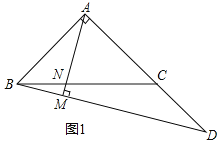
����Ŀ����ͼ����![]() �У�
�У�![]() ����DΪAC�ӳ�����һ�㣬����BD����A��
����DΪAC�ӳ�����һ�㣬����BD����A��![]() ������ΪM����BC�ڵ�N
������ΪM����BC�ڵ�N
![]() ��ͼ1����
��ͼ1����![]() ��
��![]() ����AM�ij���
����AM�ij���
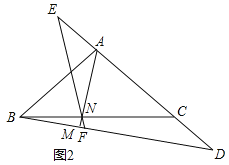
![]() ��ͼ2����E��CA���ӳ����ϣ���
��ͼ2����E��CA���ӳ����ϣ���![]() ������EN���ӳ���BD�ڵ�F����֤��
������EN���ӳ���BD�ڵ�F����֤��![]() ��
��
![]() ��
��![]() �������£���
�������£���![]() ʱ�������
ʱ�������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������y=ax2+3ax+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ��1��0����OC=3OB,

��1���������ߵĽ���ʽ��
��2������D���߶�AC�·��������ϵĶ��㣬���ı���ABCD��������ֵ��
��3������E��x���ϣ���P���������ϣ��Ƿ������A��C��E��PΪ��������ACΪһ�ߵ�ƽ���ı��Σ������ڣ�д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��Ϊ������ֱ���˶����ٶ�v(m/s)��ʱ��t(s)(0��t��40)֮��ĺ���ͼ���ݶԴ�ͼ��ķ��������⣬��ͼ���л������������ʱ���������뿪�������·��s(m)��ʱ��t(s)֮��ĺ���ͼ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=6��BC=6![]() ������P�ӵ�A��������ÿ��
������P�ӵ�A��������ÿ��![]() ����λ���ȵ��ٶ����߶�AD�˶�������Q�ӵ�D��������ÿ��2����λ���ȵ��ٶ������߶�D��O��C�˶�����֪P��Qͬʱ��ʼ�ƶ���������P����D��ʱ��P��Qͬʱֹͣ�˶������˶�ʱ��Ϊt�룮
����λ���ȵ��ٶ����߶�AD�˶�������Q�ӵ�D��������ÿ��2����λ���ȵ��ٶ������߶�D��O��C�˶�����֪P��Qͬʱ��ʼ�ƶ���������P����D��ʱ��P��Qͬʱֹͣ�˶������˶�ʱ��Ϊt�룮
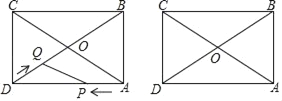
��1����t=1��ʱ����P��Q֮��ľ��룻
��2��������P��Q֮��ľ���Ϊ4����λ���ȣ���t��ֵ��
��3�����߶�PQ���е�ΪM���������˶������У�ֱ��д����M�˶�·���ij���Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+(4a��1)x��4��x�ύ�ڵ�A��B����y�ύ�ڵ�C����OC=2OB����DΪ�߶�OB��һ����(�����B�غ�)������D������DEFH����H��F���������ϣ���E��x���ϣ�
��1���������ߵĽ���ʽ��
��2��������DEFH���ܳ����ʱ�������DEFH�������
��3���ڣ�2���������£�����DEFH������������������x������ƽ��m����λ�������������DEFH�ı߽��ڵ�M��N������M��N����MNǡ��ƽ�־���DEFH���������m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳�Ϊ3����E��F�ֱ�������DC��DA���˶�����DE=DF������BF����EH��BF����ֱ���ڵ�H������CH��
��1����ͼ1������E��DC���е㣬CH��AB֮���������ϵ�� ��
��2����ͼ2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ����Ƿ����������������֤��������������˵�����ɣ�
��3����ͼ3������E��F�ֱ�������DC��DA���˶�ʱ������DH������D��ֱ��DH�Ĵ��ߣ���ֱ��BF�ڵ�K������CK����ֱ��д���߶�CK�������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��
![]() ��������ߵĶԳ��᷽���Լ���
��������ߵĶԳ��᷽���Լ���![]() ��Ľ�������
��Ľ�������
![]() ��
��![]() ʱ�������������
ʱ�������������![]() ��Ľ�������
��Ľ�������
![]() ��֪
��֪![]() ���㹹��������
���㹹��������![]() ������������������
������������������![]() ��������һ����
��������һ����![]() ������ʱ��ֱ��д��
������ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������ͼ��������A����4����3����B��2m��y1����C��6m��y2��������m��0��
��1����y1��y2=4ʱ����m��ֵ��
��2����ͼ������B��C�ֱ���x�ᡢy��Ĵ��ߣ��������ཻ�ڵ�D����P��x���ϣ���������PBD�������8����д����P���꣨����Ҫд�����̣���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com