
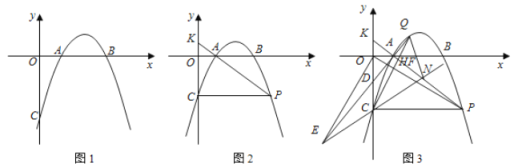
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+(4aЉ1)xЉ4гыxжсНЛгкЕуAЁЂBЃЌгыyжсНЛгкЕуCЃЌЧвOC=2OBЃЌЕуDЮЊЯпЖЮOBЩЯвЛЖЏЕу(ВЛгыЕуBжиКЯ)ЃЌЙ§ЕуDзїОиаЮDEFHЃЌЕуHЁЂFдкХзЮяЯпЩЯЃЌЕуEдкxжсЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБОиаЮDEFHЕФжмГЄзюДѓЪБЃЌЧѓОиаЮDEFHЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌОиаЮDEFHВЛЖЏЃЌНЋХзЮяЯпбизХxжсЯђзѓЦНвЦmИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌСЌНгMЁЂNЃЎШєMNЧЁКУЦНЗжОиаЮDEFHЕФУцЛ§ЃЌЧѓmЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=![]() x2+xЉ4ЃЛЃЈ2ЃЉ10ЃЛЃЈ3ЃЉmЕФжЕЮЊ
x2+xЉ4ЃЛЃЈ2ЃЉ10ЃЛЃЈ3ЃЉmЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕуCЕФзјБъЃЌгЩOCЃН2OBЃЌПЩЭЦГіЕуBзјБъЃЌНЋЕуBзјБъДњШыyЃНax2ЃЋЃЈ4aЉ1ЃЉxЉ4ПЩЧѓГіaЕФжЕЃЌМДПЩаДГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуDзјБъЮЊЃЈxЃЌ0ЃЉЃЌгУКЌxЕФДњЪ§ЪНБэЪОГіОиаЮDEFHЕФжмГЄЃЌгУКЏЪ§ЕФЫМЯыЧѓГіШЁЦфзюДѓжЕЪБxЕФжЕЃЌМДЧѓГіЕуDЕФзјБъЃЌНјвЛВНПЩЧѓГіОиаЮDEFHЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМЃЌСЌНгBHЃЌEHЃЌDFЃЌЩшEHгыDFНЛгкЕуGЃЌЙ§ЕуGзїBHЕФЦНааЯпЃЌНЛEDгкMЃЌНЛHFгкЕуNЃЌдђжБЯпMNНЋОиаЮDEFHЕФУцЛ§ЗжГЩЯрЕШЕФСНАыЃЌвРДЮЧѓГіжБЯпBHЃЌMNЕФНтЮіЪНЃЌдйЧѓГіЕуMЕФзјБъЃЌМДПЩЕУГіmЕФжЕЃЎ
НтЃКЃЈ1ЃЉдкХзЮяЯпyЃНax2ЃЋ(4aЉ1)xЉ4жаЃЌ
ЕБxЃН0ЪБЃЌyЃНЉ4ЃЌ
ЁрC(0ЃЌЉ4)ЃЌ
ЁрOCЃН4ЃЎ
ЁпOCЃН2OBЃЌ
ЁрOBЃН2ЃЌ
ЁрB(2ЃЌ0)ЃЌ
НЋB(2ЃЌ0)ДњШыyЃНax2ЃЋ(4aЉ1)xЉ4ЃЌЕУЃКaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2ЃЋxЉ4ЃЛ
x2ЃЋxЉ4ЃЛ
ЃЈ2ЃЉЩшЕуDзјБъЮЊ(xЃЌ0)ЃЎ
ЁпЫФБпаЮDEFHЮЊОиаЮЃЌ
ЁрH(xЃЌ![]() x2ЃЋxЉ4)ЃЎ
x2ЃЋxЉ4)ЃЎ
ЁпyЃН![]() x2ЃЋxЉ4ЃН
x2ЃЋxЉ4ЃН![]() (xЃЋ1)2Љ
(xЃЋ1)2Љ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊxЃНЉ1ЃЌ
ЁрЕуHЕНЖдГЦжсЕФОрРыЮЊxЃЋ1ЃЌ
гЩЖдГЦадПЩжЊDEЃНFHЃН2xЃЋ2ЃЌ
ЁрОиаЮDEFHЕФжмГЄCЃН2(2xЃЋ2)ЃЋ2(Љ![]() x2ЉxЃЋ4)ЃНЉx2ЃЋ2xЃЋ12ЃНЉ(xЉ1)2ЃЋ13ЃЌ
x2ЉxЃЋ4)ЃНЉx2ЃЋ2xЃЋ12ЃНЉ(xЉ1)2ЃЋ13ЃЌ
ЁрЕБxЃН1ЪБЃЌОиаЮDEFHжмГЄШЁзюДѓжЕ13ЃЌ
ЁрДЫЪБH(1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЁрHFЃН2xЃЋ2ЃН4ЃЌDHЃН![]() ЃЌ
ЃЌ
ЁрSОиаЮDEFHЃНHFDHЃН4ЁС![]() ЃН10ЃЛ
ЃН10ЃЛ
ЃЈ3ЃЉШчЭМЃЌ
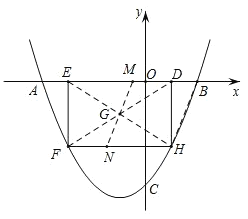
СЌНгBHЃЌEHЃЌDFЃЌЩшEHгыDFНЛгкЕуGЃЌ
Й§ЕуGзїBHЕФЦНааЯпЃЌНЛEDгкMЃЌНЛHFгкЕуNЃЌдђжБЯпMNНЋОиаЮDEFHЕФУцЛ§ЗжГЩЯрЕШЕФСНАыЃЌ
гЩЃЈ2ЃЉжЊЃЌХзЮяЯпЖдГЦжсЮЊxЃНЉ1ЃЌH(1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЁрG(Љ1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЩшжБЯпBHЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌ
НЋЕуB(2ЃЌ0)ЃЌH(1ЃЌЉ![]() )ДњШыЃЌ
)ДњШыЃЌ
ЕУЃК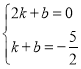 ЃЌНтЕУЃК
ЃЌНтЕУЃК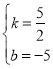 ЃЌ
ЃЌ
ЁржБЯпBHЕФНтЮіЪНЮЊyЃН![]() xЉ5ЃЌ
xЉ5ЃЌ
ЁрПЩЩшжБЯпMNЕФНтЮіЪНЮЊyЃН![]() xЃЋnЃЌ
xЃЋnЃЌ
НЋЕу(Љ1ЃЌЉ![]() )ДњШыЃЌЕУnЃН
)ДњШыЃЌЕУnЃН![]() ЃЌ
ЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊyЃН![]() xЃЋ
xЃЋ![]() ЃЌ
ЃЌ
ЕБyЃН0ЪБЃЌxЃНЉ![]() ЃЌ
ЃЌ
ЁрM(Љ![]() ЃЌ0)ЃЎ
ЃЌ0)ЃЎ
ЁпB(2ЃЌ0)ЃЌ
ЁрНЋХзЮяЯпбизХxжсЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌ
ИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌ
СЌНгMЁЂNЃЌдђMNЧЁКУЦНЗжОиаЮDEFHЕФУцЛ§ЃЌ
ЁрmЕФжЕЮЊ![]() ЃЎ
ЃЎ


 ИпжаБиЫЂЬтЯЕСаД№АИ
ИпжаБиЫЂЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
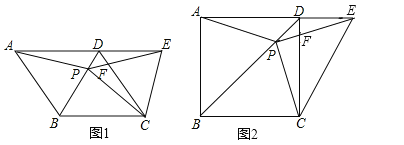
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌADЁЭBCгкЕуDЃЎ
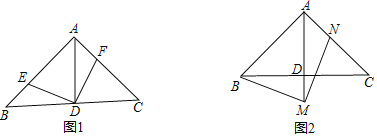
ЃЈ1ЃЉШчЭМ1ЃЌЕуEЃЌFдкABЃЌACЩЯЃЌЧвЁЯEDF=90ЁуЃЎЧѓжЄЃКBE=AFЃЛ
ЃЈ2ЃЉЕуMЃЌNЗжБ№дкжБЯпADЃЌACЩЯЃЌЧвЁЯBMN=90ЁуЃЎШчЭМ2ЃЌЕБЕуMдкADЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃКAB+AN=![]() AMЃЛ
AMЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
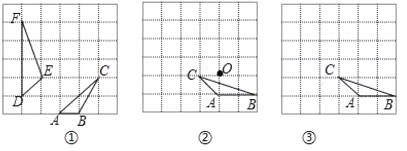
ЁОЬтФПЁПШчЭМЃЌдк![]() ЕФе§ЗНаЮЗНИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЪЧ1ЃЌЖЅЕуЖМдкЭјИёЯпЕФНЛЕуДІЕФШ§НЧаЮЃЌ
ЕФе§ЗНаЮЗНИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЪЧ1ЃЌЖЅЕуЖМдкЭјИёЯпЕФНЛЕуДІЕФШ§НЧаЮЃЌ![]() ЪЧвЛИіИёЕуШ§НЧаЮЃЎ
ЪЧвЛИіИёЕуШ§НЧаЮЃЎ
ЃЈ1ЃЉдкЭМ1жаЃЌЧыХаЖЯ![]() гы
гы![]() ЪЧЗёЯрЫЦЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёЯрЫЦЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкЭМ2ЃЌжаЃЌвдOЮЊЮЛЫЦжааФЃЌдйЛвЛИіИёЕуШ§НЧаЮЃЌЪЙЫћгы![]() ЕФЮЛЫЦБШЮЊ
ЕФЮЛЫЦБШЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЭМ3жаЃЌЧыЛГіЫљгаТњзуЬѕМўЕФИёЕуШ§НЧаЮЃЌЫќгы![]() ЯрЫЦЃЌЧвгавЛЬѕЙЋЙВБпКЭвЛИіЙЋЙВНЧЃЎ
ЯрЫЦЃЌЧвгавЛЬѕЙЋЙВБпКЭвЛИіЙЋЙВНЧЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
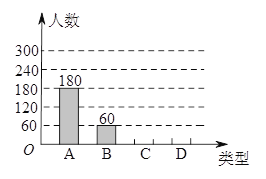
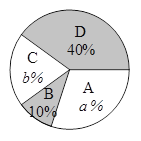
ЁОЬтФПЁПЁАЖЫЮчНкЁБЪЧЮвЙњЕФДЋЭГМбНкЃЌУёМфРњРДгаГдЁАєезгЁБЕФЯАЫзЃЎЮвЪаФГЪГЦЗГЇЮЊСЫНтЪаУёЖдШЅФъЯњСПНЯКУЕФШтЯкєеЁЂЖЙЩГЯкєеЁЂКьдцЯкєеЁЂЕАЛЦЯкєеЃЈвдЯТЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЉетЫФжжВЛЭЌПкЮЖєезгЕФЯВАЎЧщПіЃЌдкНкЧАЖдФГОгУёЧјЪаУёНјааСЫГщбљЕїВщЃЌВЂНЋЕїВщЧщПіЛцжЦГЩШчЯТСНЗљЭГМЦЭМ
ЧыИљОнвдЩЯаХЯЂЛиД№ЃК
ЃЈ1ЃЉБОДЮВЮМгГщбљЕїВщЕФОгУёга________ШЫЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃКa=________ЃЌb=_________ЃЌВЂАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєгаЭтаЭЭъШЋЯрЭЌЕФAЃЌBЃЌCЃЌDєеИївЛИіЃЌжѓЪьКѓЃЌаЁЭѕГдСЫСНИіЃЌгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЫћЕкЖўИіГдЕНЕФЧЁКУЪЧCєеЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
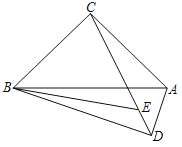
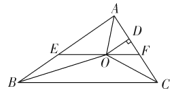
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧЁїABCЕФаББпABЯТЗНгавЛЖЏЕуDЃЌЁЯADBЃН90ЁуЃЌBEЦНЗжЁЯABDНЛCDгкЕуEЃЌдђ![]() ЕФзюаЁжЕЪЧ_____ЃЎ
ЕФзюаЁжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌХзЮяЯп
ЮЊзјБъдЕуЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЮЊХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕФКсзјБъЮЊ4ЃЌЧѓ
ЕФКсзјБъЮЊ4ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕу![]() ЮЊЖдГЦжсгвВрЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊЖдГЦжсгвВрЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎСЌНг
ЃЎСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() бгГЄЯпгкЕу
бгГЄЯпгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌбгГЄ
ЪБЃЌбгГЄ![]() НЛХзЮяЯпгкЕу
НЛХзЮяЯпгкЕу![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌНЛЯпЖЮ
ЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌНЋЩфЯп
ЃЌНЋЩфЯп![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ45ЁуЃЌЕУЕНЩфЯп
ФцЪБеыа§зЊ45ЁуЃЌЕУЕНЩфЯп![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпABНЛЁбOгкCЁЂDСНЕуЃЌCEЪЧЁбOЕФжБОЖЃЌCFЦНЗжЁЯACEНЛЁбOгкЕуFЃЌСЌНгEFЃЌЙ§ЕуFзїFGЁЮEDНЛABгкЕуGЃЎ
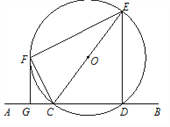
ЃЈ1ЃЉЧѓжЄЃКжБЯпFGЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєFGЃН4ЃЌЁбOЕФАыОЖЮЊ5ЃЌЧѓЫФБпаЮFGDEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФвЛЕуЃЌЕу
ЩЯЕФвЛЕуЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌЧв
ЕФбгГЄЯпЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩ.
ЕФаЮзДЃЌВЂЫЕУїРэгЩ.
ЃЈ3ЃЉШчЭМ2ЃЌАбСтаЮ![]() ИФЮЊе§ЗНаЮ
ИФЮЊе§ЗНаЮ![]() ЃЌЦфЫћЬѕМўВЛБфЃЌжБНгаДГіЯпЖЮ
ЃЌЦфЫћЬѕМўВЛБфЃЌжБНгаДГіЯпЖЮ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЕФЪ§СПЙиЯЕ.
ЕФЪ§СПЙиЯЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() КЭ
КЭ![]() ЕФЦНЗжЯпЯрНЛгкЕу
ЕФЦНЗжЯпЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎИјГівдЯТЫФИіНсТлЃК
ЃЎИјГівдЯТЫФИіНсТлЃК
ЂйШє![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
Ђк![]() ЃЛ
ЃЛ
Ђл![]() ЦНЗж
ЦНЗж![]() ЃЛ
ЃЛ
ЂмШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФга________ЃЎ(АбЫљгае§ШЗНсТлЕФађКХЖМбЁЩЯ)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com