
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .给出以下四个结论:
.给出以下四个结论:
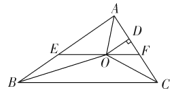
①若![]() ,
,![]() ;
;
②![]() ;
;
③![]() 平分
平分![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的有________.(把所有正确结论的序号都选上)
【答案】②③④
【解析】
运用三角形内角和定理和角平分线的定义进行计算,即可判定①;根据平行线等分线段定理和角平分线定理即可确定②;根据三角形三条角平分线交于一点,即可判定③;设O到AE的距离为h,h=OD=3,然后求三角形AEF的面积即可判定④.
解:∵![]()
∴∠ABC+∠ACB=180°-80°=100°
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB) =50°
(∠ABC+∠ACB) =50°
∴![]() =180°-∠OBC+∠OCB=130°,故①错误;
=180°-∠OBC+∠OCB=130°,故①错误;
∵![]()
∴![]()
∵OB平分∠ABC
∴∠ABO=∠OBC
∵![]()
∴∠EOB=∠OBC
∴∠EOB=∠EBO
∴OE=BE,同理:CF=OF
∴![]() ,即②正确;
,即②正确;
∵![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]()
∴O为三个角的角平分线的交点,即![]() 平分
平分![]() ,故③正确;
,故③正确;
设O到AE的距离为h,即高为h
∵O为三个角的角平分线的交点
∴h=CD=3
∴S△AEF= S△AOE+ S△AOF=![]() ×AE·h+
×AE·h+![]() ×AF·CD=
×AF·CD=![]() ×3(AE+AF)
×3(AE+AF)
∵AE+AF=8
∴S△AEF=12,故④正确;
故答案为②③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B,与y轴交于点C,且OC=2OB,点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH,点H、F在抛物线上,点E在x轴上.
(1)求抛物线的解析式;
(2)当矩形DEFH的周长最大时,求矩形DEFH的面积;
(3)在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N.若MN恰好平分矩形DEFH的面积,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
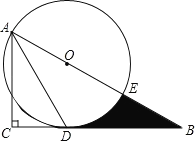
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售两种椅子,普通椅子价格是每把180元,实木椅子的价格是每把400元.
(1)该公司在2019年第一月销售了两种椅子共900把,销售总金额达到了272000元,求两种椅了各销售了多少把?
(2)第二月正好赶上市里开展家俱展销活动,公司决定将普通椅子每把降30元后销售,实木椅子每把降价2a%(a>0)后销售,在展销活动的第一周,该公司的普通椅子销售量比上一月全月普通椅子的销售量多了![]() a%:实木椅子的销售量比第一月全月实木椅子的销售量多了a%,这一周两种椅子的总销售金额达到了251000元,求a的值.
a%:实木椅子的销售量比第一月全月实木椅子的销售量多了a%,这一周两种椅子的总销售金额达到了251000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水8吨以内(包括8吨)和用水8吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
(1)求出自来水公司在这两个用水范围内的收费标准;
(2)若芳芳家6月份共交水费28.1元,请写出用水量超过8吨时应交水费y(元)与用水量x(吨)之间的函数关系,并求出芳芳家6月份的用水量.
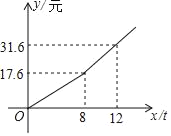
查看答案和解析>>
科目:初中数学 来源: 题型:
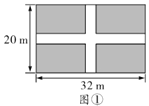
【题目】为了美化校园,某校要在如图①所示的长![]() ,宽
,宽![]() 的矩形地面上修等宽的人行道,余下的部分进行绿化.
的矩形地面上修等宽的人行道,余下的部分进行绿化.
(1)设人行道宽为![]() ,用含
,用含![]() 的式子表示绿化面积;
的式子表示绿化面积;
(2)如果要使绿化面积为![]() ,求出此时人行道的宽;
,求出此时人行道的宽;
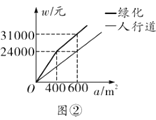
(3)已知某园林公司修筑人行道、绿化的造价![]() (元)、
(元)、![]() (元)与修建面积
(元)与修建面积![]() 之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于
之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于![]() 且不超过
且不超过![]() ,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
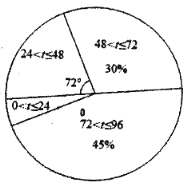
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.
去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图
今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
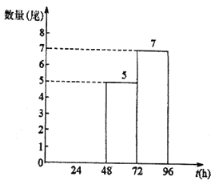
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 | 中位数 | 众数 | 方差 | |
去年 | 64.2 | 68 | 73 | 715.6 |
今年 | 56.2 | a | 68 | 629.7 |
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于![]() BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )

A. BE=EFB. EF∥CDC. AE平分∠BEFD. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
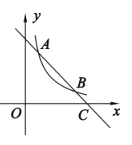
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com