
【题目】中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.
去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图
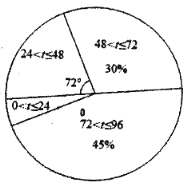
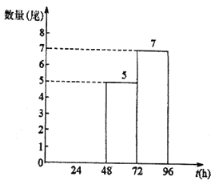
今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 | 中位数 | 众数 | 方差 | |
去年 | 64.2 | 68 | 73 | 715.6 |
今年 | 56.2 | a | 68 | 629.7 |
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
【答案】(1)64;(2)见详解;(3)1560
【解析】
(1)先求出去年落在48<t≤72内的数据个数,从而根据“今年落在24<t≤48内的“声呐鲟”比去年多1尾”得到今年落在48<t≤72内的数据个数,继而根据各时间段的数据和为20求出24<t≤48内的数据个数,从而补全图形,最后根据中位数的概念求解可得;
(2)从平均数上看去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,答案不唯一,合理即可;
(3)用总数量乘以放流72小时内通过监测站A的对应的百分比求出去年、今年的数量,求和即可得.
解:(1)去年落在48<t≤72内的数据有20×![]() (个),
(个),
∴今年落在48<t≤72内的数据为5,
则今年24<t≤48内的“声呐鲟”数量为20-(5+5+7)=3,
补全图形如下:
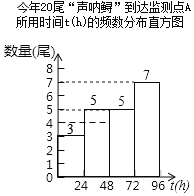
∵今年“声呐鲟”到达下游监测点时间的第10、11个数据为60、68,
∴a=![]() ,
,
故答案为:64.
(2)选择平均数,
由表可知,去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,
所以今年“声呐鲟”从长江到海洋的适应情况更好(答案不唯一,合理即可).
(3)去年和今年在放流72小时内中华鲟通过监测站A的数量为
1300×(1-45%)+1300×![]() =715+845=1560(尾).
=715+845=1560(尾).


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
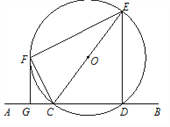
(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
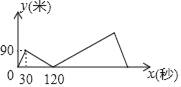
【题目】甲、乙两人在1200米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进,已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,x(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与x函数关系,那么,乙到达终点后_____秒与甲相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
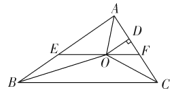
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .给出以下四个结论:
.给出以下四个结论:
①若![]() ,
,![]() ;
;
②![]() ;
;
③![]() 平分
平分![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的有________.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
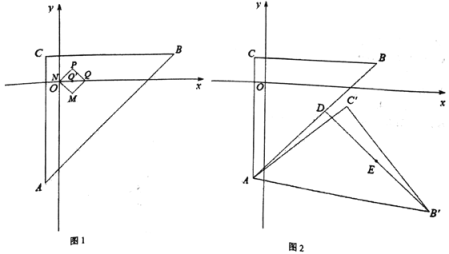
【题目】对于平面直角坐标系中的两个图形K1和K2,给出如下定义:点G为图形K1上任意一点,点H为K2图形上任意一点,如果G,H两点间的距离有最小值,则称这个最小值为图形K1和K2的“近距离”。如图1,已知△ABC,A(-1,-8),B(9,2),C(-1,2),边长为![]() 的正方形PQMN,对角线NQ平行于x轴或落在x轴上.
的正方形PQMN,对角线NQ平行于x轴或落在x轴上.
(1)填空:
①原点O与线段BC的“近距离”为 ;
②如图1,正方形PQMN在△ABC内,中心O’坐标为(m,0),若正方形PQMN与△ABC的边界的“近距离”为1,则m的取值范围为 ;
(2)已知抛物线C:![]() ,且-1≤x≤9,若抛物线C与△ABC的“近距离”为1,求a的值;
,且-1≤x≤9,若抛物线C与△ABC的“近距离”为1,求a的值;
(3)如图2,已知点D为线段AB上一点,且D(5,-2),将△ABC绕点A顺时针旋转α(0<α≤180),将旋转中的△ABC记为△AB’C’,连接DB’,点E为DB’的中点,当正方形PQMN中心O’坐标为(5,-6),直接写出在整个旋转过程中点E运动形成的图形与正方形PQMN的“近距离”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行了抽样调查,从两个城市中所有的饮料自动售卖机中分别随机抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25,45,44,22,10,28,61,18,38,45,78,45,58,32,16,72
乙:48,52,21,25,33,12,42,39,41,42,33,44,33,18,68,72
整理、描述数据,对销售金额进行分组,各组的频数如下:
销售金额 |
|
|
|
|
甲 | 3 | 5 | 5 | 3 |
乙 | 2 | 6 |
|
|
分析数据,两组样本数据的平均数、中位数如下表所示:
城市 | 中位数 | 平均数 | 众数 |
甲 |
| 39.8 | 45 |
乙 | 40 | 38.9 |
|
请根据以上信息,回答下列问题:
(1)填空:![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________
________
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com