
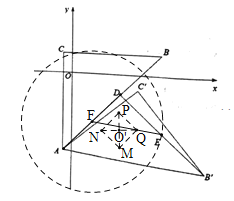
����Ŀ������ƽ��ֱ������ϵ�е�����ͼ��K1��K2���������¶��壺��GΪͼ��K1������һ�㣬��HΪK2ͼ��������һ�㣬���G��H�����ľ�������Сֵ����������СֵΪͼ��K1��K2����������������ͼ1����֪��ABC��A��-1��-8����B��9,2����C��-1,2�����߳�Ϊ![]() ��������PQMN���Խ���NQƽ����x�������x���ϣ�
��������PQMN���Խ���NQƽ����x�������x���ϣ�
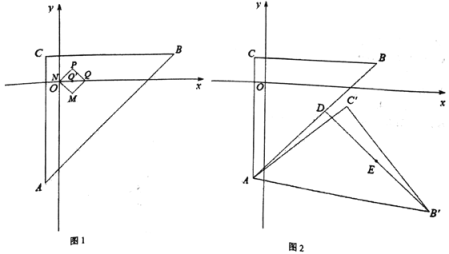
��1����գ�
��ԭ��O���߶�BC������������Ϊ ��
����ͼ1��������PQMN����ABC�ڣ�����O������Ϊ��m��0������������PQMN����ABC�ı߽������������Ϊ1����m��ȡֵ��ΧΪ ��
��2����֪������C��![]() ����-1��x��9����������C����ABC������������Ϊ1����a��ֵ��
����-1��x��9����������C����ABC������������Ϊ1����a��ֵ��
��3����ͼ2����֪��DΪ�߶�AB��һ�㣬��D��5��-2��������ABC�Ƶ�A˳ʱ����ת����0<����180��������ת�е���ABC��Ϊ��AB��C��������DB������EΪDB�����е㣬��������PQMN����O������Ϊ��5��-6����ֱ��д����������ת�����е�E�˶��γɵ�ͼ����������PQMN��������������
���𰸡���1����2����![]() ����2��
����2��![]() ��
��![]() ����3����E�˶��γɵ�ͼ����������PQMN�ġ���������Ϊ
����3����E�˶��γɵ�ͼ����������PQMN�ġ���������Ϊ![]() ��
��
��������
��1�����ɴ��߶���̣����ɵõ��𰸣�
�ڸ������⣬�ҳ�������PQMN����ABC�ı߽������������Ϊ1�����ٽ�㣬Ȼ��ֱ����m����Сֵ�����ֵ�����ɵõ�m��ȡֵ��Χ��
��2���������⣬���������ABC�ġ������롱Ϊ1ʱ���ɷ�Ϊ�������������C�������ߵľ���Ϊ1����CD=1�������������߶�AB�ľ���Ϊ1ʱ����GH=1���ֱ����a��ֵ�����ɵõ��𰸣�
��3���������⣬ȡAB���е�F������EF�����EF�ij��ȣ�Ȼ��������⣬�����F����Q�����꣬���FQ�ij��ȣ����ɵõ�EQ�ij��ȣ����ɵõ��𰸣�
�⣺��1���١�B��9��2����C��![]() ��2����
��2����
���B��C����������ͬ��
���߶�BC��x�ᣬ
��ԭ��O���߶�BC����̾���Ϊ2��
��ԭ��O���߶�BC�ġ������롱Ϊ2��
�ʴ�Ϊ��2��
�ڡ�A��-1��-8����B��9��2����C��-1��2����
���߶�BC��x�ᣬ�߶�AC��y�ᣬ
��AC=BC=10����ABC�ǵ���ֱ�������Σ�
����N���O�غ�ʱ����N���߶�AC����̾���Ϊ1��
��������PQMN����ABC�ı߽�ġ������롱Ϊ1��
��ʱmΪ��Сֵ��
�������εı߳�Ϊ![]() ��
��
�ɹ��ɶ������ã�![]() ��
��
��![]() ��
��![]() ����ȥ����
����ȥ����
����Q���߶�AB�ľ���Ϊ1ʱ����ʱmΪ���ֵ����ͼ��
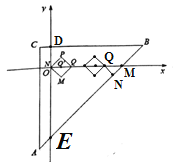
��QN=1����QMN�ǵ���ֱ�������Σ�
��QM=![]() ��
��
��BD=9����BDE�ǵ���ֱ�������Σ�
��DE=9��
�ߡ�OEM�ǵ���ֱ�������Σ�
��OE=OM=7��
��m�����ֵΪ��![]() ��
��
��m��ȡֵ��ΧΪ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2��������C��![]() ����
����![]() ����������C����ABC������������Ϊ1��
����������C����ABC������������Ϊ1��
�����֪����C�������ߵľ���Ϊ1ʱ����ͼ��
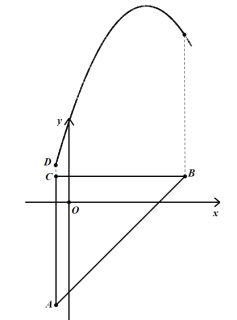
�ߵ�C������Ϊ��![]() ��2����
��2����
�൫D������Ϊ��![]() ��3����
��3����
�ѵ�D����![]() �У���
����
![]() ��
��
��ã�![]() ��
��
���߶�AB�������ߵľ���Ϊ1ʱ��������Ϊ1����ͼ����GH=1��
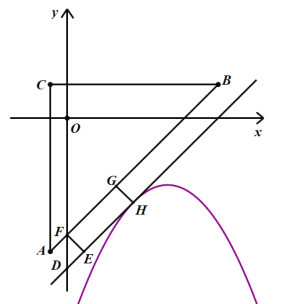
��H���������ϣ�����H��AB��ƽ���ߣ��߶�AB��y���ཻ�ڵ�F����FE��EH������ΪE��
��EF=GH=1��
�ߡ�FDE=��A=45�㣬
��![]() ��
��
�ߵ�A��-1��-8����B��9��2������ֱ��ABΪ![]() ��
��
��![]() ����ã�
����ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪ��![]() ��
��
��ֱ��EH�Ľ���ʽΪ��![]() ��
��
������![]() ��
��![]() ����
����
![]() ��
��
�����ã�![]() ��
��
��ֱ��EH����������һ�����㣬
��![]() ��
��
��ã�![]() ��
��
�ۺ�������a��ֵΪ��![]() ��
��![]() ��
��
��3�������⣬ȡAB���е�F������EF����ͼ��
�ߵ�A��-1��-8����B��9��2����
��![]() ��
��
��![]() �У�F��AD���е㣬��E��
�У�F��AD���е㣬��E��![]() ���е㣬
���е㣬
��![]() ��
��
�ߵ�D������Ϊ��5��-2����A��-1��-8����
���F��������2��![]() ����
����
����������PNMQ�У����ĵ�![]() ������Ϊ��5��
��������5��![]() ����
����
���Q��������6��![]() ����
����
��![]() ��
��
��![]() ��
��
���E�˶��γɵ�ͼ����������PQMN�ġ������롱Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���3x2��3(a��b)x��4ab��0������ʵ����x1��x2�����ϵʽ��x1(x1��1)��x2(x2��1)��(x1��1)(x2��1)���ж�(a��b)2��4�Ƿ���ȷ������ȷ�������֤����������ȷ�����һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����������ӣ���ͨ���Ӽ۸���ÿ��180Ԫ��ʵľ���ӵļ۸���ÿ��400Ԫ��
(1)�ù�˾��2019���һ���������������ӹ�900�ѣ������ܽ��ﵽ��272000Ԫ�����������˸������˶��ٰѣ�
(2)�ڶ������ø������↑չ�Ҿ�չ�������˾��������ͨ����ÿ�ѽ�30Ԫ�����ۣ�ʵľ����ÿ�ѽ���2a%(a��0)�����ۣ���չ����ĵ�һ�ܣ��ù�˾����ͨ��������������һ��ȫ����ͨ���ӵ�����������![]() a%��ʵľ���ӵ��������ȵ�һ��ȫ��ʵľ���ӵ�����������a%����һ���������ӵ������۽��ﵽ��251000Ԫ����a��ֵ��
a%��ʵľ���ӵ��������ȵ�һ��ȫ��ʵľ���ӵ�����������a%����һ���������ӵ������۽��ﵽ��251000Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
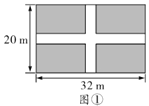
����Ŀ��Ϊ������У��ijУҪ����ͼ����ʾ�ij�![]() ����
����![]() �ľ��ε������ȿ������е������µIJ��ֽ����̻���
�ľ��ε������ȿ������е������µIJ��ֽ����̻���
��1�������е���Ϊ![]() ���ú�
���ú�![]() ��ʽ�ӱ�ʾ�̻������
��ʽ�ӱ�ʾ�̻������
��2�����Ҫʹ�̻����Ϊ![]() �������ʱ���е��Ŀ���
�������ʱ���е��Ŀ���
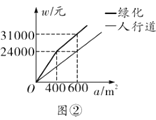
��3����֪ij�ֹ�˾�������е����̻������![]() (Ԫ)��
(Ԫ)��![]() (Ԫ)�������
(Ԫ)�������![]() ֮��ĺ�����ϵ��ͼ����ʾ�������У�����ɸù�˾�н�����Ŀ����Ҫ���������е��Ŀ��Ȳ�����
֮��ĺ�����ϵ��ͼ����ʾ�������У�����ɸù�˾�н�����Ŀ����Ҫ���������е��Ŀ��Ȳ�����![]() �Ҳ�����
�Ҳ�����![]() ����ô���е���Ϊ����ʱ���������е����̻����������ͣ���������Ϊ����Ԫ��
����ô���е���Ϊ����ʱ���������е����̻����������ͣ���������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л����ǹ���һ������������Ǵ�����������࣬���ڳ��������ں�������̬������Ӱ�죬���������½����л����о���ÿ�궨��ͨ���˹���ֳ�����������л����������ÿ��������л��������������ڰ�װ�˳�Ч���ű�ǣ����ڼ�����Ǵӳ������������Ӧ������ⲿ���л�����Ϊ�������������о����ռ������ǵ������μ���A��ʱ��t��h����������ݣ����������²�����ͳ��ͼ��ͳ�Ʊ���
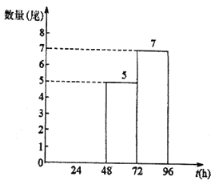
��֪�������ȥ��ֱ���20β�����������ڷ�����96Сʱ�ڵ������A����������24<t��48�ڵ�������������ȥ���1β����������48<t��72�ڵ����ݷֱ�Ϊ49��60��68��68��71��
ȥ��20β�����������������A ����ʱ��t��h��������ͳ��ͼ
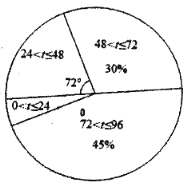
����20β�����������������A����ʱ��t��h����Ƶ���ֲ�ֱ��ͼ
���������������������A����ʱ��t��h����ͳ�Ʊ�
ƽ���� | ��λ�� | ���� | ���� | |
ȥ�� | 64.2 | 68 | 73 | 715.6 |
���� | 56.2 | a | 68 | 629.7 |
��1���벹ȫƵ���ֲ�ֱ��ͼ��������������Ϣ��գ�a= ��
��2���л��ൽ�ﺣ���ʱ��Խ�죬˵�����ӳ������������Ӧ�����Խ�ã������������Ϣ��ѡ��һ��ͳ����˵��ȥ��ͽ�������һ���л���ӳ������������Ӧ������ã�
��3��ȥ��ͽ���÷����㹲����1300β�л��࣬������������������50β������ƽ����ȥ���ڷ���72Сʱ�ڹ��ж���β�л���ͨ�����վA��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij��ѧһ��Ȥζ�˶���50������ƹ���������Ŀ�У���ƹ������������ڣ�������Ա������ס��������ƹ������һ��1����ͳ�һ��2����̨ͬ������ijʱ�̣�1���С����2���С�ķֱ�λ��50�����������![]() �غ��յ�
�غ��յ�![]() �أ�����ͬʱ������������У��ֱ��Ը��Ե��ٶ�����ֱ�߱��ܣ������е�ijʱ�̣�С��������ƹ��������
�أ�����ͬʱ������������У��ֱ��Ը��Ե��ٶ�����ֱ�߱��ܣ������е�ijʱ�̣�С��������ƹ��������![]() �أ�
�أ�![]() ��
��![]() ��
��![]() ��ͬһֱ������ƹ��������
��ͬһֱ������ƹ��������![]() �غ����ƶ�������6��ʱС���ŷ��ֲ�Ѹ�ٵ�ͷ��ԭ��ȥ��ƹ�������С�����ٶ�������С���ٶȵ�����Ѹ����
�غ����ƶ�������6��ʱС���ŷ��ֲ�Ѹ�ٵ�ͷ��ԭ��ȥ��ƹ�������С�����ٶ�������С���ٶȵ�����Ѹ����![]() ��������ȥ��С����ͷ�ͼ����ʱ����Բ��ƣ���ͼ������֮��ľ���
��������ȥ��С����ͷ�ͼ����ʱ����Բ��ƣ���ͼ������֮��ľ���![]() ���ף���С��������ʱ��
���ף���С��������ʱ��![]() ���룩֮��ĺ���ͼ����С������
���룩֮��ĺ���ͼ����С������![]() ��ʱ��С����
��ʱ��С����![]() �ػ���________�ף�
�ػ���________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ��Ե�AΪԲ�ġ�AB�ij�Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ġ�����![]() BF�ij�Ϊ�뾶�������������ڵ�M��������AM��BC�ڵ�E������EF�����н����в�һ���������ǣ�������
BF�ij�Ϊ�뾶�������������ڵ�M��������AM��BC�ڵ�E������EF�����н����в�һ���������ǣ�������

A. BE��EFB. EF��CDC. AEƽ�֡�BEFD. AB��AE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x��2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н�����ȷ���ǣ�������
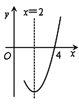
A.��x��2ʱ��y��x���������B.a��b��c��0
C.�����߹��㣨��4��0��D.4a��b��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
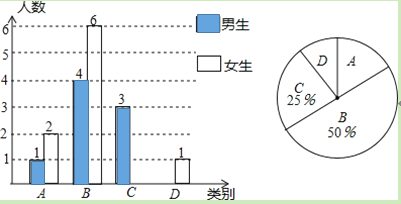
��1�����ε�����C��Ů����______����D��������______���������������ͳ��ͼ����������
��2����������ͳ��ͼ��D��ռ��Բ�Ľ���______��
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com