
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
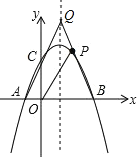
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
【答案】(1)y=-x2+2x+3;(2)点Q的坐标为(1,5)或(1.-5).
【解析】
(1)点A、B、C的坐标已知,只需运用待定系数法就可求出抛物线的解析式;
(2)由四边形POP′B为菱形可得PO=PB,从而有∠POB=∠PBO.由点Q在抛物线的对称轴上可得QA=QB,从而有∠QAB=∠QBA.由△QAB与△POB相似可得∠PBO=∠QBA,从而可得点Q、P、B共线.由PO=PB可得点P在OB的垂直平分线上,从而可得xP=![]() ,代入抛物线即可求出点P的坐标,然后根据相似三角形的性质,即可得到点Q的坐标;
,代入抛物线即可求出点P的坐标,然后根据相似三角形的性质,即可得到点Q的坐标;
(1)∵A(-1,0)、B(3,0)、C(0,3)在抛物线y=ax2+bx+c上,
∴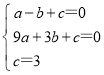 ,
,
解得 .
.
∴抛物线的解析式为y=-x2+2x+3;
(2)∵四边形POP′B为菱形,
∴PO=PB,
∴∠POB=∠PBO.
∵点Q在抛物线的对称轴上,
∴QA=QB,
∴∠QAB=∠QBA.
由△QAB与△POB相似可得∠PBO=∠QBA,
∴当Q点在x轴上方时,点Q、P、B共线.
∵PO=PB,
∴点P在OB的垂直平分线上,
∴xP=![]() ,
,
此时yP=-![]() ,
,
点P的坐标为(![]() ).
).
∵△QAB~△POB,
∴![]() ,
,
∵yP=![]() ,AB=4,OB=3,
,AB=4,OB=3,
∴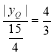 ,
,
∴|yQ|=5,
∴yQ=±5,
∵抛物线的对称轴为x=-![]() =1,
=1,
∴点Q的坐标为(1,5)或(1.-5).


科目:初中数学 来源: 题型:
【题目】中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
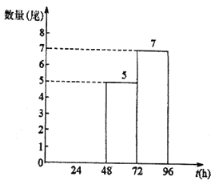
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.
去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图
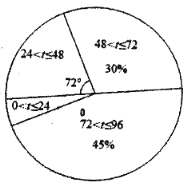
今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 | 中位数 | 众数 | 方差 | |
去年 | 64.2 | 68 | 73 | 715.6 |
今年 | 56.2 | a | 68 | 629.7 |
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
查看答案和解析>>
科目:初中数学 来源: 题型:
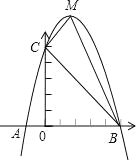
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积![]() .
.
(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
查看答案和解析>>
科目:初中数学 来源: 题型:
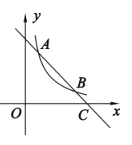
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
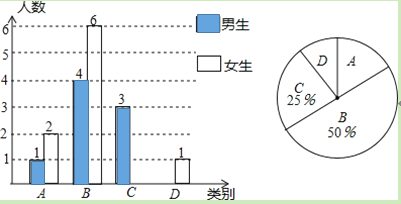
(1)本次调查中C类女生有______名,D类男生有______名;将上面的条形统计图补充完整;
(2)计算扇形统计图中D所占的圆心角是______;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
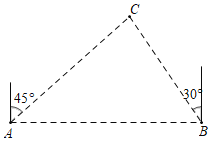
【题目】如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为__海里(精确到1海里,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com