
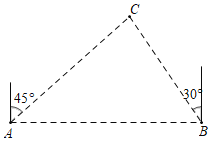
【题目】如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为__海里(精确到1海里,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
科目:初中数学 来源: 题型:
【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行了抽样调查,从两个城市中所有的饮料自动售卖机中分别随机抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25,45,44,22,10,28,61,18,38,45,78,45,58,32,16,72
乙:48,52,21,25,33,12,42,39,41,42,33,44,33,18,68,72
整理、描述数据,对销售金额进行分组,各组的频数如下:
销售金额 |
|
|
|
|
甲 | 3 | 5 | 5 | 3 |
乙 | 2 | 6 |
|
|
分析数据,两组样本数据的平均数、中位数如下表所示:
城市 | 中位数 | 平均数 | 众数 |
甲 |
| 39.8 | 45 |
乙 | 40 | 38.9 |
|
请根据以上信息,回答下列问题:
(1)填空:![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________
________
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
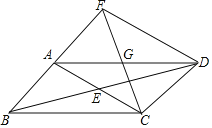
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
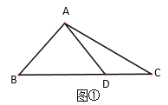
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
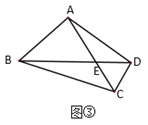
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
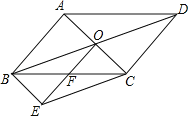
(1)求证:F为BC中点.
(2)若OB⊥AC,OF=1,求平行四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
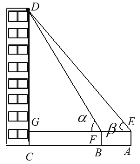
【题目】某兴趣小组用高为1米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为∠β=30![]() ,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60
,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60![]() .测得A,B之间的距离为4米,建筑物CD的高度为______ .
.测得A,B之间的距离为4米,建筑物CD的高度为______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
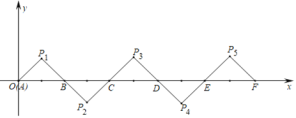
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
A.(4039,-1)
B.(4039,1)
C.(2020,-1)
D.(2020,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com