
【题目】如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
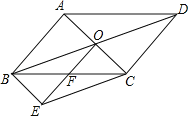
(1)求证:F为BC中点.
(2)若OB⊥AC,OF=1,求平行四边形ABCD的周长.
【答案】(1)见解析;(2)平行四边形ABCD的周长为8.
【解析】
(1)先证明OB=OD,再证得EC//OD,EC=OD,进而得到OB//EC,OB=EC,说明四边形OBEC为平行四边形,最后根据平行四边形的性质即可证明;
(2)先证明四边形ABCD平行四边形,再证明平行四边形DOEC是矩形,求得BC,即可求得菱形ABCD的周长.
(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵四边形DOEC为平行四边形,
∴OD∥EC,OD=EC,
∴EC∥OB,EC=OB,
∴四边形OBEC为平行四边形,
∴BF=CF,即F为BC中点;
(2)解:∵四边形ABCD是平行四边形,OB⊥AC,
∴四边形ABCD是菱形,
∵四边形OBEC为平行四边形,OB⊥AC,
∴四边形OBEC为矩形,
∴BC=OE=2OF,
∵OF=1,
∴BC=2,
∴平行四边形ABCD的周长=4BC=8.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于![]() BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )

A. BE=EFB. EF∥CDC. AE平分∠BEFD. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
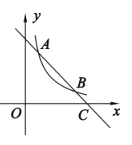
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
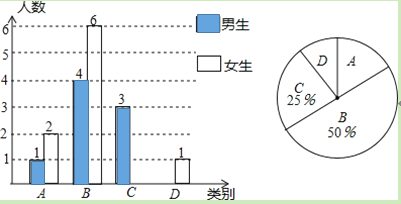
(1)本次调查中C类女生有______名,D类男生有______名;将上面的条形统计图补充完整;
(2)计算扇形统计图中D所占的圆心角是______;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为__海里(精确到1海里,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
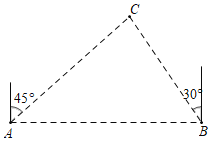
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形.
(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称: .
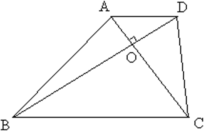
(2)如图,在梯形ABCD中,AD∥BC,AC⊥BD,垂足为O.
求证:![]() ,即四边形ABCD是等平方和四边形.
,即四边形ABCD是等平方和四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划6月底组织员工到某地旅游,参加旅游的人数估计为5-20人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠.请你帮他们算一算该公司应选择哪一家旅行社支付的旅游费用较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com