
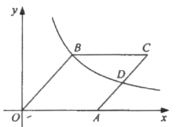
【题目】如图,菱形![]() 的顶点
的顶点![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() (
(![]() )的图像经过顶点
)的图像经过顶点![]() ,和边
,和边![]() 的中点
的中点![]() .若
.若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
作BE⊥x轴,DF⊥x轴,根据菱形的性质可得OB∥AC,OB=AB=AC=6,进而可得AD=![]() AC=3,由平行可得△BOE∽△DAF,进而可得
AC=3,由平行可得△BOE∽△DAF,进而可得![]() ,设AF=a,DF=b,则OE=2a,BE=2b,由此可表示出点B、D的坐标,代入函数关系式可得方程,进而可求得k的值.
,设AF=a,DF=b,则OE=2a,BE=2b,由此可表示出点B、D的坐标,代入函数关系式可得方程,进而可求得k的值.
解:如图,分别过点B、D作BE⊥x轴,DF⊥x轴,垂足分别为E、F,
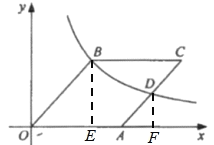
则∠BEO=∠DFA=90°,
∵在菱形AOBC中,
∴OB∥AC,OB=AB=AC=6,
∵点D为AC的中点,
∴AD=![]() AC=3,
AC=3,
∵OB∥AC,
∴∠BOE=∠DAF,
∴△BOE∽△DAF,
∴![]() ,
,
∴设AF=a,DF=b,
则OE=2a,BE=2b,
∴点D(6+a,b),点B(2a,2b),
∵点B、D均在反比例函数图像上,
∴将点D(6+a,b),点B(2a,2b)代入![]() 得:
得:
b(6+a)=2a·2b=k,
解得a=2,
∴OE=2a=4,
在Rt△BOE中,BE=![]() ,
,
∴点B(4,![]() ),
),
∴![]() .
.
故选:D.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
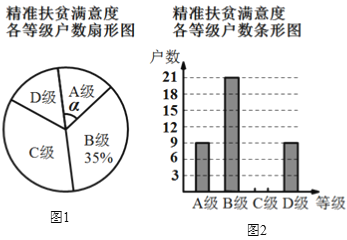
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
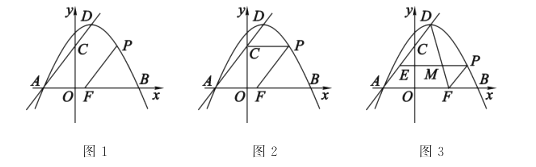
【题目】综合与探究:
如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() ,
,![]() 为对称轴右侧抛物线的一个动点,直线
为对称轴右侧抛物线的一个动点,直线![]() 与
与![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的函数表达式及点
的函数表达式及点![]() 的坐标;
的坐标;
(2)如图2,当![]() 轴时,将
轴时,将![]() 以每秒1个单位长度的速度沿
以每秒1个单位长度的速度沿![]() 轴的正方向平移,当点
轴的正方向平移,当点![]() 与点
与点![]() 重合时停止平移.设平移
重合时停止平移.设平移![]() 秒时,在平移过程中
秒时,在平移过程中![]() 与四边形
与四边形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)如图3,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②试探究点![]() 在运动过程中,是否存在值
在运动过程中,是否存在值![]() ,使四边形
,使四边形![]() 是菱形?若存在,请直接写出点
是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
(k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
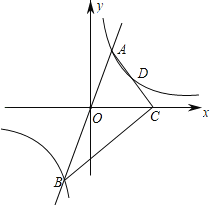
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
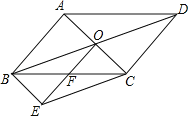
(1)求证:F为BC中点.
(2)若OB⊥AC,OF=1,求平行四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.己知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.
(1)每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元?
(2)学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:________.
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】姐妹两人在50米的跑道上进行短路比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为a米/秒、b米/秒.
(1)如果两人重新开始比赛,姐姐从起点向后退3米,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com