
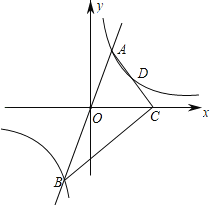
【题目】如图,过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
(k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
科目:初中数学 来源: 题型:
【题目】在某中学一次趣味运动会50米托盘乒乓球接力项目中(即乒乓球放入托盘内,参赛队员用手托住托盘运送乒乓球),初一(1)班和初一(2)班同台竞技,某时刻,1班的小敏和2班的小文分别位于50米赛道的起点![]() 地和终点
地和终点![]() 地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在
地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在![]() 地(
地(![]() 、
、![]() 、
、![]() 在同一直线上且乒乓球落在
在同一直线上且乒乓球落在![]() 地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往
地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往![]() 地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离
地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离![]() (米)与小敏出发的时间
(米)与小敏出发的时间![]() (秒)之间的函数图象,则当小敏到达
(秒)之间的函数图象,则当小敏到达![]() 地时,小文离
地时,小文离![]() 地还有________米.
地还有________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
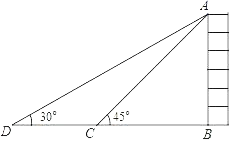
【题目】如图所示,初三数学兴趣小组同学为了测量垂直于水平地面的一座大厦AB的高度,一测量人员在大厦附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了60米后到达D处,在D处测得A处的仰角大小为30°,则大厦AB的高度约为多少米?(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
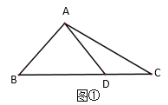
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
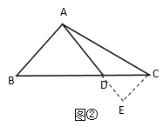
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
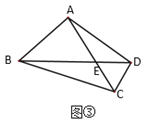
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
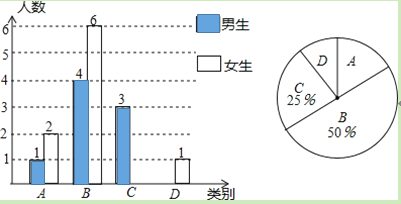
(1)本次调查中C类女生有______名,D类男生有______名;将上面的条形统计图补充完整;
(2)计算扇形统计图中D所占的圆心角是______;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
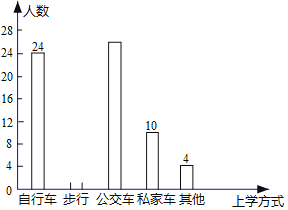
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)延长线段![]() 到
到![]() ,延长线段
,延长线段![]() 到
到![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①判断![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com