
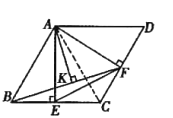
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)延长线段![]() 到
到![]() ,延长线段
,延长线段![]() 到
到![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①判断![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ;(3)①
;(3)①![]() 是等边三角形,见解析;②
是等边三角形,见解析;②![]()
【解析】
(1)连接EF,AC,由菱形的性质,可证![]() ,然后得到
,然后得到![]() 为等边三角形,由解直角三角形得到
为等边三角形,由解直角三角形得到![]() ,即可得到答案;
,即可得到答案;
(2)由菱形的性质和等边三角形的性质,求出AF的长度,然后得到BF的长度,然后由相似三角形的性质,得到![]() ,即可求出答案;
,即可求出答案;
(3)①由等边三角形的性质,先证明![]() ,然后得到
,然后得到![]() ,然后得到
,然后得到![]() ,即可得到答案;
,即可得到答案;
②由三角形的面积公式得到![]() ,然后得到
,然后得到![]() 为等腰直角三角形,再由解直角三角形的性质,即可求出答案.
为等腰直角三角形,再由解直角三角形的性质,即可求出答案.
解:(1)![]() ;
;
理由:∵四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() .
.
连接![]() ,
,![]()
![]()
在![]() 中,
中,![]()
![]() ,
,
![]()
(2)如图:

∵四边形![]() 是菱形,
是菱形,![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() .
.
![]() ,垂足为
,垂足为![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
![]()
![]() ,垂足为
,垂足为![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
(3)如图:
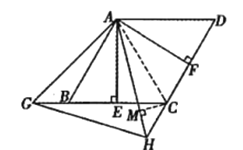
①![]() 是等边三角形.
是等边三角形.
理由:连接![]() .
.
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
又![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() 为等边三角形;
为等边三角形;
②![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.
又![]() ,
,
![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数y=![]() (k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
(k>0)的图象交于点A,B两点,在x轴有一点C(3,0),AC⊥BC,连结AC交反比例函数图象于点D,若AD=CD,则k的值为( )
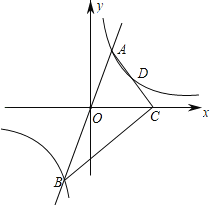
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】姐妹两人在50米的跑道上进行短路比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为a米/秒、b米/秒.
(1)如果两人重新开始比赛,姐姐从起点向后退3米,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2-2x+c与x轴的一个交点是(1,0).
(1)C的值为_______;
(2)选取适当的数据补填下表,并在平面直角坐标系内描点画出该抛物线的图像;
|
|
|
|
| |||
|
|
|
|
(3)根据所画图像,写出y>0时x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(方法回顾)连接三角形任意两边中点的线段叫三角形的中位线,探索三角形中位线的性质,方法如下:
①如图1,D、E分别是AB、AC中点,延长DE到F,使EF=DE,连接CF;
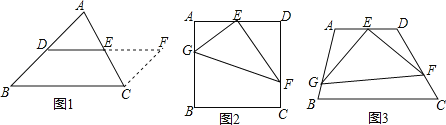
②证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到线段DE与BC的位置关系和数量关系分别为_______、________;
(2)(初步运用)如图2,正方形ABCD中,E为边AD中点,G、F分别在边AB、CD上,且AG=2,DF=3,∠GEF=90°,求GF长.
(3)(拓展延伸)如图3,四边形ABCD中,∠A=100°,∠D=110°,E为AD中点,G、F分别为AB、CD边上的点,若AG=2,DF=![]() ,∠GEF=90°,求GF长.
,∠GEF=90°,求GF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 个质地、大小完全相同的小球上分别标有数字
个质地、大小完全相同的小球上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .先将标有数字
.先将标有数字![]() ,
,![]() ,
,![]() 的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现从第一个盒子里随机取出一个小球,再从第二个盒子里随机取出一个小球.两次分别用x、y来表示.
的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现从第一个盒子里随机取出一个小球,再从第二个盒子里随机取出一个小球.两次分别用x、y来表示.
(1)请利用列表或画树状图的方法中的一种方法,求(x,y)所有可能出现的结果总数;
(2)求取出的两个小球上的数字之和等于![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
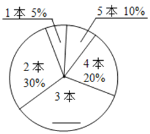
【题目】某校为迎接中华人民共和国成立七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.德育处对九年级学生九月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,绘制了两幅不完整的统计图(如图所示).
(1)请补全两幅统计图;本次抽样调查抽取了名学生;
(2)求本次所抽取学生九月份“读书量”的平均数;
(3)已知该校九年级有500名学生,请你估计该校九年级学生中,九月份“读书量”为5本的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com