
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈ4ЃЌ0ЃЉЃЌжБЯпy2=mx+nЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃК
Ђй2a+b=0ЃЛЂкabcЃО0ЃЛЂлЗНГЬax2+bx+c=3гаСНИіЯрЕШЕФЪЕЪ§ИљЃЛЂмХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЛЂнЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃМy1ЃЌ
Цфжае§ШЗЕФЪЧЃЈ ЃЉ

A. ЂйЂкЂл B. ЂйЂлЂм C. ЂйЂлЂн D. ЂкЂмЂн
ЁОД№АИЁПC
ЁОНтЮіЁП
ЪдЬтНтЮіЃКЁпХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=-![]() =1ЃЌ
=1ЃЌ
Ёр2a+b=0ЃЌЫљвдЂйе§ШЗЃЛ
ЁпХзЮяЯпПЊПкЯђЯТЃЌ
ЁрaЃМ0ЃЌ
Ёрb=-2aЃО0ЃЌ
ЁпХзЮяЯпгыyжсЕФНЛЕудкxжсЩЯЗНЃЌ
ЁрcЃО0ЃЌ
ЁрabcЃМ0ЃЌЫљвдЂкДэЮѓЃЛ
ЁпХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌ
Ёрx=1ЪБЃЌЖўДЮКЏЪ§газюДѓжЕЃЌ
ЁрЗНГЬax2+bx+c=3гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЫљвдЂле§ШЗЃЛ
ЁпХзЮяЯпгыxжсЕФвЛИіНЛЕуЮЊЃЈ4ЃЌ0ЃЉ
ЖјХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=1ЃЌ
ЁрХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЃЈ-2ЃЌ0ЃЉЃЌЫљвдЂмДэЮѓЃЛ
ЁпХзЮяЯпy1=ax2+bx+cгыжБЯпy2=mx+nЃЈmЁй0ЃЉНЛгкAЃЈ1ЃЌ3ЃЉЃЌBЕуЃЈ4ЃЌ0ЃЉ
ЁрЕБ1ЃМxЃМ4ЪБЃЌy2ЃМy1ЃЌЫљвдЂне§ШЗЃЎ
ЙЪбЁCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
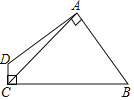
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌABЃНADЃЌACЃН6ЃЌЁЯDABЃНЁЯDCBЃН90ЁуЃЌдђЫФБпаЮABCDЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCЃЌДЙзуЮЊDЃЌAD=CDЃЌЕуEдкADЩЯЃЌDE=BDЃЌMЁЂNЗжБ№ЪЧABЁЂCEЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADBЁеЁїCDEЃЛ
ЃЈ2ЃЉЧѓЁЯMDNЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЖЈвхЃКШчЙћвЛИіШ§НЧаЮвЛЬѕБпЩЯЕФИпЕШгкетЬѕБпЃЌФЧУДетИіШ§НЧаЮНазіЁАЕШИпЕзЁБШ§НЧаЮЃЌетЬѕБпНазіетИіШ§НЧаЮЕФЁАЕШЕзЁБЃЎ

ЃЈ1ЃЉИХФюРэНтЃК
ШчЭМ1ЃЌдкЁїABCжаЃЌAC=6ЃЌBC=3ЃЌЁЯACB=30ЁуЃЌЪдХаЖЯЁїABCЪЧЗёЪЧЁБЕШИпЕзЁБШ§НЧаЮЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЮЪЬтЬНОПЃК
ШчЭМ2ЃЌЁїABCЪЧЁАЕШИпЕзЁБШ§НЧаЮЃЌBCЪЧЁБЕШЕзЁБЃЌзїЁїABCЙигкBCЫљдкжБЯпЕФЖдГЦЭМаЮЕУЕНЁїA'BCЃЌСЌНсAAЁфНЛжБЯпBCгкЕуDЃЎШєЕуBЪЧЁїAAЁфCЕФжиаФЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉгІгУЭиеЙЃК
ШчЭМ3ЃЌвбжЊl1ЁЮl2ЃЌl1гыl2жЎМфЕФОрРыЮЊ2ЃЎЁАЕШИпЕзЁБЁїABCЕФЁАЕШЕзЁБBCдкжБЯпl1ЩЯЃЌЕуAдкжБЯпl2ЩЯЃЌгавЛБпЕФГЄЪЧBCЕФ![]() БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
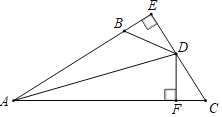
ЁОЬтФПЁПШчЭМЃЌDEЁЭABгкEЃЌDFЁЭACгкFЃЌШєBDЃНCDЁЂBEЃНCF.
(1)ЧѓжЄЃКADЦНЗжЁЯBAC.
(2)вбжЊACЃН14ЃЌBEЃН2ЃЌЧѓABЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1ЃНkxЃЋbгыЖўДЮКЏЪ§y2ЃНax2ЕФЭМЯѓНЛгкAЁЂBСНЕуЃЎ

(1)РћгУЭМжаЬѕМўЃЌЧѓСНИіКЏЪ§ЕФНтЮіЪНЃЛ
(2)ИљОнЭМЯѓаДГіЪЙy1>y2ЕФxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁї ABCжаЃЌAB=ACЃЌЁЯ BAC=90ЁуЃЌжБНЧЁЯ EPFЕФЖЅЕуPЪЧBCжаЕуЃЌСНБпPEЁЂPFЗжБ№НЛABЁЂACгкЕуEЁЂFЃЌИјГівдЯТЫФИіНсТлЃКЂйAE=CFЃЛЂкЁї EPFЪЧЕШбќжБНЧШ§НЧаЮЃЛ Ђл2SЫФБпаЮAEPF=SЁї ABCЃЛ ЂмBE+CF=EFЃЎЕБЁЯ EPFдкЁї ABCФкШЦЖЅЕуPа§зЊЪБЃЈЕуEгыAЁЂBжиКЯЃЉЃЎЩЯЪіНсТлжаЪМжее§ШЗЕФга( )

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌХзЮяЯп![]() ОЙ§ЕуMЃЈ1ЃЌ3ЃЉКЭNЃЈ3ЃЌ5ЃЉ
ОЙ§ЕуMЃЈ1ЃЌ3ЃЉКЭNЃЈ3ЃЌ5ЃЉ

ЃЈ1ЃЉЪдХаЖЯИУХзЮяЯпгыxжсНЛЕуЕФЧщПіЃЛ
ЃЈ2ЃЉЦНвЦетЬѕХзЮяЯпЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЈЉ2ЃЌ0ЃЉЃЌЧвгыyжсНЛгкЕуBЃЌЭЌЪБТњзувдAЁЂOЁЂBЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќжБНЧШ§НЧаЮЃЌЧыФуаДГіЦНвЦЙ§ГЬЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№БэЪО
ЗжБ№БэЪО![]() ВНаагы
ВНаагы![]() ЦяГЕдкЭЌвЛТЗЩЯааЪЛЕФТЗГЬ
ЦяГЕдкЭЌвЛТЗЩЯааЪЛЕФТЗГЬ![]() ЃЈЧЇРДЃЉгыЪБМф
ЃЈЧЇРДЃЉгыЪБМф![]() ЃЈаЁЪБЃЉжЎМфЕФЙиЯЕЃЎ
ЃЈаЁЪБЃЉжЎМфЕФЙиЯЕЃЎ
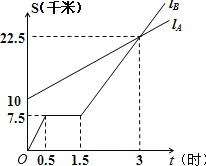
ЃЈ1ЃЉ![]() ГіЗЂЪБгы
ГіЗЂЪБгы![]() ЯрОр______ЧЇУзЃЎ
ЯрОр______ЧЇУзЃЎ
ЃЈ2ЃЉ![]() зпСЫвЛЖЮТЗКѓЃЌздааГЕЗЂЩњЙЪеЯЃЌНјаааоРэЃЌЫљгУЕФЪБМфЪЧ______аЁЪБЃЎ
зпСЫвЛЖЮТЗКѓЃЌздааГЕЗЂЩњЙЪеЯЃЌНјаааоРэЃЌЫљгУЕФЪБМфЪЧ______аЁЪБЃЎ
ЃЈ3ЃЉ![]() ГіЗЂКѓ______аЁЪБгы
ГіЗЂКѓ______аЁЪБгы![]() ЯргіЃЎ
ЯргіЃЎ
ЃЈ4ЃЉЧѓГі![]() аазпЕФТЗГЬ
аазпЕФТЗГЬ![]() гыЪБМф
гыЪБМф![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ5ЃЉШє![]() ЕФздааГЕВЛЗЂЩњЙЪеЯЃЌБЃГжГіЗЂЪБЕФЫйЖШЧАНјЃЌФЧУДМИаЁЪБгы
ЕФздааГЕВЛЗЂЩњЙЪеЯЃЌБЃГжГіЗЂЪБЕФЫйЖШЧАНјЃЌФЧУДМИаЁЪБгы![]() ЯргіЃПЯргіЕуРы
ЯргіЃПЯргіЕуРы![]() ЕФГіЗЂЕуЖрЩйЧЇУзЃПЧыЭЌбЇУЧдкЭМжаЛГіетИіЯргіЕу
ЕФГіЗЂЕуЖрЩйЧЇУзЃПЧыЭЌбЇУЧдкЭМжаЛГіетИіЯргіЕу![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com