
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
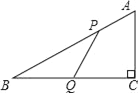
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
【答案】(1)△ABC是“等高底”三角形;(2)![]() ;(3)CD的值为
;(3)CD的值为![]() ,2
,2![]() ,2.
,2.
【解析】
(1)过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,根据30°所对的直角边等于斜边的一半可得:![]() 根据“等高底”三角形的概念即可判断.
根据“等高底”三角形的概念即可判断.
(2)点B是![]() 的重心,得到
的重心,得到![]() 设
设![]() 则
则![]()
根据勾股定理可得![]() 即可求出它们的比值.
即可求出它们的比值.
(3)分两种情况进行讨论:①当![]() 时和②当
时和②当![]() 时.
时.
(1)△ABC是“等高底”三角形;
理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,

∵∠ACB=30°,AC=6,
∴![]()
∴AD=BC=3,
即△ABC是“等高底”三角形;
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,

∴![]()
∵△ABC关于BC所在直线的对称图形是![]() ,
,
∴∠ADC=90°,
∵点B是![]() 的重心,
的重心,
∴![]()
设![]() 则
则![]()
由勾股定理得![]()
∴![]()
(3)①当![]() 时,
时,
Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,
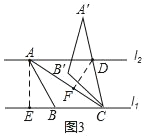
∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,![]() .
.
∴![]()
∴BE=2,即EC=4,
∴![]()
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴∠DCF=45°,
设![]()
∵l1∥l2,
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
Ⅱ.如图4,此时△ABC等腰直角三角形,

∵△ABC绕点C按顺时针方向旋转45°得到![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
②当![]() 时,
时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,
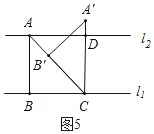
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴![]()
∴![]()
Ⅱ.如图6,作![]() 于E,则
于E,则![]()
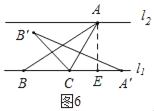
∴![]()
∴![]()
∴△ABC绕点C按顺时针方向旋转45°,得到![]() 时,点A'在直线l1上,
时,点A'在直线l1上,
∴![]() ∥l2,即直线
∥l2,即直线![]() 与l2无交点,
与l2无交点,
综上所述,CD的值为![]()


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:AE=BD;
(2)请判断△CMN的形状,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是
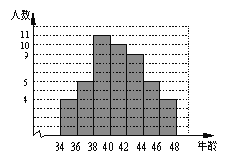
A.该学校教职工总人数是50人
B.年龄在40≤x<42小组的教职工人数占该学校总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,P是AD上一动点,连接BP,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
(1)当AB=AD,且P是AD的中点时,求证:AG=BP;
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若AB=3AD,AD=2AP,![]() 的值为 .(直接填答案)
的值为 .(直接填答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则
(1)四边形ABCD是 形;
(2)若∠B=120°,点P、E、F分别为线段AC、AD、DC上的任意1点,则PE+PF的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解答过程,然后再解答:
形如![]() 的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得![]() ,
,![]() ,那么便有:
,那么便有:![]() (a>b)
(a>b)
例如:化简![]()
解:首先把![]() 化为
化为![]() ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12
即![]() ,
,![]()
∴![]() =
=![]()
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)化简:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com