
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

【答案】见解析
【解析】试题分析:(1)由垂直的定义得到∠ADB=∠ADC=90°,根据已知条件即可得到结论;
(2)根据全等三角形的性质得到∠BAD=∠DCE,根据直角三角形的性质得到AM=DM,DN=CN,由等腰三角形的性质得到∠MAD=∠MDA,∠NCD=∠NDC,等量代换得到∠ADM=∠CDN,即可得到结论.
试题解析:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,在△ABD与△CDE中,∵AD=CD,∠ADB=∠ADC,DB=DE,∴△ABD≌△CDE;
(2)解:∵△ABD≌△CDE,∴∠BAD=∠DCE,∵M、N分别是AB、CE的中点,∴AM=DM,DN=CN,∴∠MAD=∠MDA,∠NCD=∠NDC,∴∠ADM=∠CDN,∵∠CDN+∠ADN=90°,∴∠ADM+∠ADN=90°,∴∠MDN=90°.


科目:初中数学 来源: 题型:
【题目】小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,……如图所示.
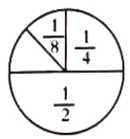
(1)如果继续这样切下去,能把这张油饼切完吗?为什么?
(2)如果依照上面的规律切了10次,那么剩下的油饼是整张油饼的几分之几?
(3)如果厨师照上述方式切了![]() 次,那么他一共将这张油饼切去了多少?
次,那么他一共将这张油饼切去了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
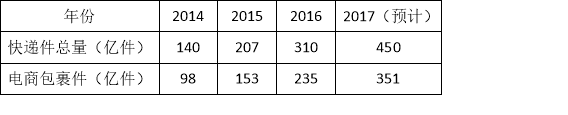
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
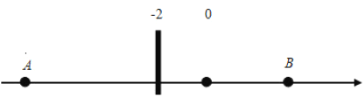
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )
①DE的最小值为1;②ADCE的面积是不变的;③在整个运动过程中,点E运动的路程为2;④在整个运动过程中,△ADE的周长先变小后变大.

A. ①③④ B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
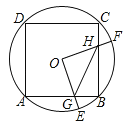
【题目】(2016湖北省咸宁市)如图,边长为4的正方形ABCD内接于点O,点E是![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
①![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为![]() .
.
其中正确的是________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只小虫子落在数轴上的某点![]() ,第一次从
,第一次从![]() 向左跳一个单位到
向左跳一个单位到![]() ,第二次从
,第二次从![]() 向右跳
向右跳![]() 个单位到
个单位到![]() ,第三次从
,第三次从![]() 向左跳
向左跳![]() 个单位到
个单位到![]() ,第四次从
,第四次从![]() 向右跳
向右跳![]() 个单位到
个单位到![]() ,按以上规律跳了
,按以上规律跳了![]() 次时,它落在数轴上的点
次时,它落在数轴上的点![]() 所表示的数恰好是2019,则这只小虫的初始位置
所表示的数恰好是2019,则这只小虫的初始位置![]() 所在的数是_____.
所在的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示a、b.
![]()
(1)对照数轴填写下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A、B两点的距离 |
(2)若A、B两点间的距离记为d,问:d和a、b有何数量关系?
(3)在数轴上标出所有符合条件的整数点,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小?最小值为多少?
取得的值最小?最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com