
【题目】已知点A、B在数轴上分别表示a、b.
![]()
(1)对照数轴填写下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A、B两点的距离 |
(2)若A、B两点间的距离记为d,问:d和a、b有何数量关系?
(3)在数轴上标出所有符合条件的整数点,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小?最小值为多少?
取得的值最小?最小值为多少?
【答案】(1)见解析;(2)d=|a-b|;(3)符合条件的整数点有:-5、-4、-3、-2、-1、0、1、2、3、4、5;和为0;(4)当-3≤x≤1时,![]() 取最小值为4;
取最小值为4;
【解析】
(1)根据数轴即可得答案;
(2)根据两点间得距离即可得答案;
(3)根据数轴即可得整数点,求和即可得答案;
(4)![]() 的值最小,即是x到1的距离和到-3的距离得和最小,则x应在-3和1之间得线段上.
的值最小,即是x到1的距离和到-3的距离得和最小,则x应在-3和1之间得线段上.
(1)根据数轴填表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A、B两点的距离 | 2 | 6 | 10 | 2 | 12 | 0 |
(2)∵|6-4|=2,|-6-0|=6,|-6-4|=10,|-6-(-4)|=2,|2-(-10)|=12,|-1.5-(-1.5)|=0,
∴A、B两点的距离=两数差的绝对值,
∴d=|a-b|.
(3)设这个点为P,
∵点P到5和-5的距离之和为10,
∴|p-5|+|p-(-5)|=10,
∴符合条件的整数点有:-5、-4、-3、-2、-1、0、1、2、3、4、5,
数轴如下:
![]()
∴所有这些整数的和为-5+-4+-3+-2+-1+0+1+2+3+4+5=0.
(4)∵在数轴上![]() 的几何意义是:表示有理数x的点到1及到-3的距离之和,
的几何意义是:表示有理数x的点到1及到-3的距离之和,
∴x应在-3和1之间得线段上,
∴当-3≤x≤1时,它取最小值为4;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
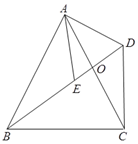
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED, EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
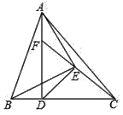
A. ①③B. ①②④C. ①②③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 为等边三角形,点 D、E 分别在边 BC、AC 上,且 AE=CD,AD 与 BE相交于点 F.则∠DFE 的度数为_____°;
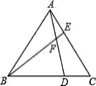
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C任作一射线CM,交AB于M,分别过A,B作AE⊥CM,BF⊥CM,垂足分别为E,F.

(1)求证:∠ACE=∠CBF;
(2)求证:AE=CF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示)
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,
那么S△ABC = .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com