
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж10ЗжЃЉ
ЮЪЬтЬсГіЃКгУnИљЯрЭЌЕФФОАєДювЛИіШ§НЧаЮЃЈФОАєЮоЪЃгрЃЉЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃП
ЮЪЬтЬНОПЃКВЛЗСМйЩшФмДюГЩ![]() жжВЛЭЌЕФЕШбќШ§НЧаЮЃЌЮЊЬНОП
жжВЛЭЌЕФЕШбќШ§НЧаЮЃЌЮЊЬНОП![]() жЎМфЕФЙиЯЕЃЌЮвУЧПЩвдДгЬиЪтШыЪжЃЌЭЈЙ§ЪдбщЁЂЙлВьЁЂРрБШЃЌзюКѓЙщФЩЁЂВТВтЕУГіНсТлЃЎ
жЎМфЕФЙиЯЕЃЌЮвУЧПЩвдДгЬиЪтШыЪжЃЌЭЈЙ§ЪдбщЁЂЙлВьЁЂРрБШЃЌзюКѓЙщФЩЁЂВТВтЕУГіНсТлЃЎ
ЬНОПвЛЃК
гУ3ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФШ§НЧаЮЃП
ДЫЪБЃЌЯдШЛФмДюГЩвЛжжЕШбќШ§НЧаЮЁЃЫљвдЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
гУ4ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФШ§НЧаЮЃП
жЛПЩЗжГЩ1ИљФОАєЁЂ1ИљФОАєКЭ2ИљФОАєетвЛжжЧщПіЃЌВЛФмДюГЩШ§НЧаЮ
ЫљвдЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
гУ5ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФШ§НЧаЮЃП
ШєЗжГЩ1ИљФОАєЁЂ1ИљФОАєКЭ3ИљФОАєЃЌдђВЛФмДюГЩШ§НЧаЮ
ШєЗжЮЊ2ИљФОАєЁЂ2ИљФОАєКЭ1ИљФОАєЃЌдђФмДюГЩвЛжжЕШбќШ§НЧаЮ
ЫљвдЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
гУ6ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФШ§НЧаЮЃП
ШєЗжГЩ1ИљФОАєЁЂ1ИљФОАєКЭ4ИљФОАєЃЌдђВЛФмДюГЩШ§НЧаЮ
ШєЗжЮЊ2ИљФОАєЁЂ2ИљФОАєКЭ2ИљФОАєЃЌдђФмДюГЩвЛжжЕШбќШ§НЧаЮ
ЫљвдЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
злЩЯЫљЪіЃЌПЩЕУБэЂй
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
ЬНОПЖўЃК
гУ7ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃП
ЃЈЗТееЩЯЪіЬНОПЗНЗЈЃЌаДГіНтД№Й§ГЬЃЌВЂАбНсЙћЬюдкБэЂкжаЃЉ
ЗжБ№гУ8ИљЁЂ9ИљЁЂ10ИљЯрЭЌЕФФОАєДюГЩвЛИіШ§НЧаЮЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃП
ЃЈжЛашАбНсЙћЬюдкБэЂкжаЃЉ
| 7 | 8 | 9 | 10 |
|
ФуВЛЗСЗжБ№гУ11ИљЁЂ12ИљЁЂ13ИљЁЂ14ИљЯрЭЌЕФФОАєМЬајНјааЬНОПЃЌЁЁ
НтОіЮЪЬтЃКгУ![]() ИљЯрЭЌЕФФОАєДювЛИіШ§НЧаЮЃЈФОАєЮоЪЃгрЃЉЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃП
ИљЯрЭЌЕФФОАєДювЛИіШ§НЧаЮЃЈФОАєЮоЪЃгрЃЉЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃП
ЃЈЩш![]() ЗжБ№ЕШгк
ЗжБ№ЕШгк![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪЧећЪ§ЃЌАбНсЙћЬюдкБэЂлжаЃЉ
ЪЧећЪ§ЃЌАбНсЙћЬюдкБэЂлжаЃЉ
|
|
|
|
|
|
ЮЪЬтгІгУЃКгУ2016ИљЯрЭЌЕФФОАєДювЛИіШ§НЧаЮЃЈФОАєЮоЪЃгрЃЉЃЌФмДюГЩЖрЩйжжВЛЭЌЕФЕШбќШ§НЧаЮЃПЃЈвЊЧѓаДГіНтД№Й§ГЬЃЉ
ЦфжаУцЛ§зюДѓЕФЕШбќШ§НЧаЮУПИібќгУСЫ__________________ИљФОАєЁЃЃЈжЛЬюНсЙћЃЉ
ЁОД№АИЁПn=7ЃЌm=2ЃЛ503ИіЃЛ672ЃЎ
ЁОНтЮіЁП
ЪдЬт(1)ЁЂИљОнИјГіЕФНтЬтЗНЗЈЕУГіД№АИЃЛ(2)ЁЂИљОнЬтвтНЋБэИёЬюаДЭъећЃЛгІгУЃК(1)ЁЂИљОнЬтвтЕУГіkЕФжЕЃЌДгЖјЕУГіШ§НЧаЮЕФИіЪ§ЃЛИљОнШ§НЧаЮЕФаджЪЕУГіД№АИ.
ЪдЬтНтЮіЃКЬНОПЖў
(1)ЁЂШєЗжГЩ1ИљФОАєЁЂ1ИљФОАєКЭ5ИљФОАєЃЌдђВЛФмДюГЩШ§НЧаЮ
ШєЗжЮЊ2ИљФОАєЁЂ2ИљФОАєКЭ3ИљФОАєЃЌдђФмДюГЩвЛжжЕШбќШ§НЧаЮ
ШєЗжЮЊ3ИљФОАєЁЂ3ИљФОАєКЭ1ИљФОАєЃЌдђФмДюГЩвЛжжЕШбќШ§НЧаЮ
(2)ЁЂЫљвдЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
| 7 | 8 | 9 | 10 |
| 2 | 1 | 2 | 2 |
|
|
|
|
|
|
|
|
|
|
ЮЪЬтгІгУЃК(1)ЁЂЁп2016=4ЁС504 Ыљвдk=504ЃЌ дђПЩвдДюГЩk-1=503ИіВЛЭЌЕФЕШбќШ§НЧаЮЃЛ
(2)ЁЂ 672



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќМИФъЃЌЫцзХЕчзгЩЬЮёЕФПьЫйЗЂеЙЃЌЁАЕчЩЬАќЙќМўЁБеМЁАПьЕнМўЁБзмСПЕФБШР§ж№ФъдіГЄЃЌИљОнЦѓвЕВЦБЈЃЌФГЭјеОЕУЕНШчЯТЭГМЦБэЃК
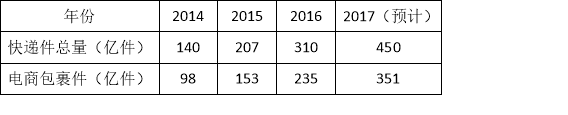
ЃЈ1ЃЉЧыбЁдёЪЪЕБЕФЭГМЦЭМЃЌУшЪі2014Љ2017ФъЁАЕчЩЬАќЙќМўЁБеМЕБФъЁАПьЕнМўЁБзмСПЕФАйЗжБШЃЈОЋШЗЕН1%ЃЉЃЛ
ЃЈ2ЃЉШє2018ФъЁАПьЕнМўЁБзмСПНЋДяЕН675вкМўЃЌЧыЙРМЦЦфжаЁАЕчЩЬАќЙќМўЁБдМЮЊЖрЩйвкМўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжЛаЁГцзгТфдкЪ§жсЩЯЕФФГЕу![]() ЃЌЕквЛДЮДг
ЃЌЕквЛДЮДг![]() ЯђзѓЬјвЛИіЕЅЮЛЕН
ЯђзѓЬјвЛИіЕЅЮЛЕН![]() ЃЌЕкЖўДЮДг
ЃЌЕкЖўДЮДг![]() ЯђгвЬј
ЯђгвЬј![]() ИіЕЅЮЛЕН
ИіЕЅЮЛЕН![]() ЃЌЕкШ§ДЮДг
ЃЌЕкШ§ДЮДг![]() ЯђзѓЬј
ЯђзѓЬј![]() ИіЕЅЮЛЕН
ИіЕЅЮЛЕН![]() ЃЌЕкЫФДЮДг
ЃЌЕкЫФДЮДг![]() ЯђгвЬј
ЯђгвЬј![]() ИіЕЅЮЛЕН
ИіЕЅЮЛЕН![]() ЃЌАДвдЩЯЙцТЩЬјСЫ
ЃЌАДвдЩЯЙцТЩЬјСЫ![]() ДЮЪБЃЌЫќТфдкЪ§жсЩЯЕФЕу
ДЮЪБЃЌЫќТфдкЪ§жсЩЯЕФЕу![]() ЫљБэЪОЕФЪ§ЧЁКУЪЧ2019ЃЌдђетжЛаЁГцЕФГѕЪМЮЛжУ
ЫљБэЪОЕФЪ§ЧЁКУЪЧ2019ЃЌдђетжЛаЁГцЕФГѕЪМЮЛжУ![]() ЫљдкЕФЪ§ЪЧ_____ЃЎ
ЫљдкЕФЪ§ЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуAЁЂBдкЪ§жсЩЯЗжБ№БэЪОaЁЂbЃЎ
![]()
ЃЈ1ЃЉЖдееЪ§жсЬюаДЯТБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AЁЂBСНЕуЕФОрРы |
ЃЈ2ЃЉШєAЁЂBСНЕуМфЕФОрРыМЧЮЊdЃЌЮЪЃКdКЭaЁЂbгаКЮЪ§СПЙиЯЕЃП
ЃЈ3ЃЉдкЪ§жсЩЯБъГіЫљгаЗћКЯЬѕМўЕФећЪ§ЕуЃЌЪЙЫќЕН5КЭ-5ЕФОрРыжЎКЭЮЊ10ЃЌВЂЧѓЫљгаетаЉећЪ§ЕФКЭЃЛ
ЃЈ4ЃЉШєЕуCБэЪОЕФЪ§ЮЊxЃЌЕБЕуCдкЪВУДЮЛжУЪБЃЌ![]() ШЁЕУЕФжЕзюаЁЃПзюаЁжЕЮЊЖрЩйЃП
ШЁЕУЕФжЕзюаЁЃПзюаЁжЕЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
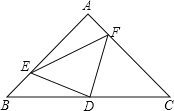
ЁОЬтФПЁПвбжЊЃКШ§НЧаЮABCжа,ЁЯA=90ЃЌAB=ACЃЌDЮЊBCЕФжаЕуЃЌШчЭМЃЌEЃЌFЗжБ№ЪЧABЃЌACЩЯЕФЕуЃЌЧвBE=AFЃЌЧѓжЄЃКЁїDEFЮЊЕШбќжБНЧШ§НЧаЮ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєХзЮяЯпLЃКy=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌabcЁй0ЃЉгыжБЯпlЖМОЙ§yжсЩЯЕФЭЌвЛЕуЃЌЧвХзЮяЯпLЕФЖЅЕудкжБЯпlЩЯЃЌдђГЦДЮХзЮяЯпLгыжБЯпlОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌВЂЧвНЋжБЯпlНазіХзЮяЯпLЕФЁАТЗЯпЁБЃЌХзЮяЯпLНазіжБЯпlЕФЁАДјЯпЁБЃЎ
ЃЈ1ЃЉШєЁАТЗЯпЁБlЕФБэДяЪНЮЊy=2xЉ4ЃЌЫќЕФЁАДјЯпЁБLЕФЖЅЕуЕФКсзјБъЮЊЉ1ЃЌЧѓЁАДјЯпЁБLЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћХзЮяЯпy=mx2Љ2mx+mЉ1гыжБЯпy=nx+1ОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌЧѓmЃЌnЕФжЕЃЛ
ЃЈ3ЃЉЩшЃЈ2ЃЉжаЕФЁАДјЯпЁБLгыЫќЕФЁАТЗЯпЁБlдкyжсЩЯЕФНЛЕуЮЊAЃЎвбжЊЕуPЮЊЁАДјЯпЁБLЩЯЕФЕуЃЌЕБвдЕуPЮЊдВаФЕФдВгыЁАТЗЯпЁБlЯрЧагкЕуAЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
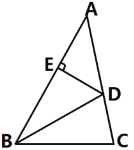
ЁОЬтФПЁПдкЁїABCжаЃЌBDЦНЗжЁЯABCЃЌНЛACгкЕуDЃЌDEЁЭABгкЕуEЃЌAB=3cmЃЌBC=2.5cmЃЌЁїABDЕФУцЛ§ЮЊ2cm2,дђSЁїABC=____________cm2ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХШЫУЧОМУЪеШыЕФВЛЖЯЬсИпЃЌЦћГЕвбдНРДдНЖрЕиНјШыЕНИїИіМвЭЅЃЎФГДѓаЭГЌЪаЮЊЛКНтЭЃГЕФбЮЪЬтЃЌНЈжўЩшМЦЪІЬсЙЉСЫТЅЖЅЭЃГЕГЁЕФЩшМЦЪОвтЭМЃЎАДЙцЖЈЃЌЭЃГЕГЁЦТЕРПкЩЯЦТвЊеХЬљЯоИпБъжОЃЌвдБуИцжЊГЕСОФмЗёАВШЋЪЛШыЃЎШчЭМЃЌЕиУцЫљдкЕФжБЯпMEгыТЅЖЅЫљдкЕФжБЯпACЪЧЦНааЕФЃЌCDЕФКёЖШЮЊ0.5mЃЌЧѓГіЦћГЕЭЈЙ§ЦТЕРПкЕФЯоИпDFЕФГЄЃЈНсЙћОЋШЗЕН0.1mЃЌsin28ЁуЁж0.47ЃЌcos28ЁуЁж0.88ЃЌtan28ЁуЁж0.53ЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10cmЃЌBC=6cmЃЌШєЖЏЕуPДгЕуCПЊЪМЃЌАДCЁњAЁњBЁњCЕФТЗОЖдЫЖЏЃЌЧвЫйЖШЮЊУПУы1cmЃЌЩшГіЗЂЕФЪБМфЮЊtУыЁЃ
(1)ГіЗЂ2УыКѓЃЌЧѓЁїABPЕФжмГЄЁЃ
(2)ЕБtЮЊМИУыЪБЃЌBPЦНЗжЁЯABC?
(3)ЮЪtЮЊКЮжЕЪБЃЌЁїBCPЮЊЕШбќШ§НЧаЮ?
(4)СэгавЛЕуQЃЌДгЕуCПЊЪМЃЌАДCЁњBЁњAЁњCЕФТЗОЖдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌШєPЁЂQСНЕуЭЌЪБГіЗЂЃЌЕБPЁЂQжагавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЁЃЕБtЮЊКЮжЕЪБЃЌжБЯпPQАбЁїABCЕФжмГЄЗжГЩЯрЕШЕФСНВПЗж?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com