
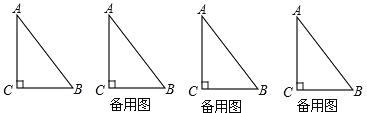
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
(1)出发2秒后,求△ABP的周长。
(2)当t为几秒时,BP平分∠ABC?
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
【答案】(1)16+2![]() ;(2)t=3秒时,AP平分∠CAB;(3)当t为6s或12s或10.8s或13s时,△BCP为等腰三角形;(4)当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.
;(2)t=3秒时,AP平分∠CAB;(3)当t为6s或12s或10.8s或13s时,△BCP为等腰三角形;(4)当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.
【解析】
(1)由勾股定理求出AC=8 cm,动点P从点C开始,出发2秒后,则CP=2 cm,AP=6 cm,由勾股定理求出PB,即可得出结果;
(2)过点P作PD⊥AB于点D,由HL证明Rt△APD≌Rt△APC,得出AD=AC=6cm,因此BD=10-6=4cm,设PC=x cm,则PB=(8-x)cm,由勾股定理得出方程,解方程即可;
(3)分两种情况:①若P在边AC上时,BC=CP=6cm,此时用的时间为6s;
②若P在AB边上时,有三种情况:
i若使BP=CB=6cm,此时AP=4cm,P运动的路程为4+8=12cm,用的时间为12时;
ii)若CP=BC=6cm,过C作CD⊥AB于点D,根据面积法求得高CD=4.8cm,求出BP=2PD=7.2cm,得出P运动的路程为18-7.2=10.8cm,即可得出结果;
ⅲ)若BP=CP,则∠PCB=∠B,证出PA=PC得出PA=PB=5cm,得出P的路程为13cm,即可得出结果;
(4)分两种情况:①当P、Q没相遇前:如图6,P点走过的路程为t,Q走过的路程为2t,根据题意得出方程,解方程即可;
②当P、Q没相遇后:当P点在AB上,Q在AC上,则AP=t-8,AQ=2t-16,根据题意得出方程,解方程即可;即可得出结果.
(1)如图1,由∠C=90,AB=10cm,BC=6cm,
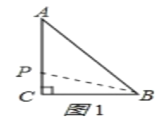
∴AC=8 cm,
∵动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2 cm,AP=6 cm,
∵∠C=90°,
∴由勾股定理得PB=![]() =2
=2![]() cm,
cm,
∴△ABP的周长为:AP+PB+AB=(16+2![]() ) cm.
) cm.
(2)如图2所示,过点P作PD⊥AB于点D,
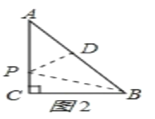
∵AP平分∠CAB,
∴PD=PC.
在Rt△APD与Rt△APC中,
![]() ,
,
∴Rt△APD≌Rt△APC(HL),
∴AD=AC=6 cm,
∴BD=106=4 cm.
设PC=x cm,则PB=(8x)cm
在Rt△BPD中,PD2+BD2=PB2,
即x2+42=(8x)2,
解得:x=3,
∴当t=3秒时,AP平分∠CAB;
(3)①如图3,若P在边AC上时,BC=CP=6cm,
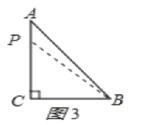
此时用的时间为6s,△BCP为等腰三角形
②若P在AB边上时,有三种情况:
i)如图4,若使BP=CB=6cm,此时AP=4cm,P运动的路程为4+8=12cm,
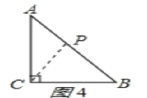
所以用的时间为12s时,△BCP为等腰三角形;
ii)如图5,若CP=BC=6cm,
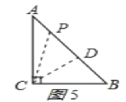
过C作CD⊥AB于点D,根据面积法得:高CD=4.8cm,
在Rt△PCD中,PD=3.6cm,∴BP=2PD=7.2cm,
∴P运动的路程为187.2=10.8cm,
∴用的时间为10.8s时,△BCP为等腰三角形;
ⅲ)如图6,若BP=CP,则∠PCB=∠B,
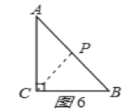
∵∠ACP+∠BCP=90°,∠B+∠A=90°,
∴∠ACP=∠A,
∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
综上所述,当t为6s或12s或10.8s或13s时,△BCP为等腰三角形;
(4)分两种情况:①当P、Q没相遇前:如图7,
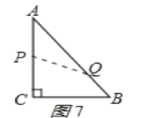
P点走过的路程为tcm,Q走过的路程为2tcm,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t=12,
∴t=4s;
②当P、Q没相遇后:如图8,
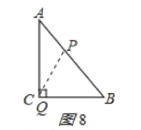
当P点在AB上,Q在AC上,则AP=t8,AQ=2t16,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t8+2t16=12,
∴t=12s,
∴当t为4秒或12秒时,直线PQ把△ABC的周长分成相等的两部分.


科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
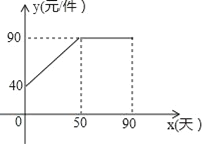
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示)
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,
那么S△ABC = .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?


把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点![]() 处,即
处,即![]() ,据以上操作,易证明
,据以上操作,易证明![]() ≌
≌![]() ,所以
,所以![]() ,又因为
,又因为![]() >∠B,所以∠C>∠B.
>∠B,所以∠C>∠B.
感悟与应用:
(1)如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;
(2)如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,
① 求证:∠B+∠D=180°;
② 求AB的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
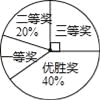
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
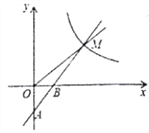
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)求AM的长度;
(3)P是x轴上一点,当AM⊥PM时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
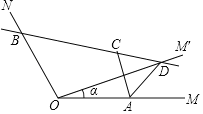
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:
①AD=CD;
②∠ACD的大小随着α的变化而变化;
③当α=30°时,四边形OADC为菱形;
④△ACD面积的最大值为![]() a2;
a2;
其中正确的是_____.(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com