
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() 、
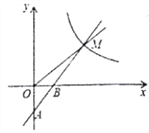
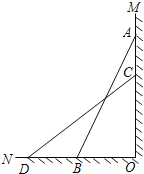
、![]() 两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)求AM的长度;
(3)P是x轴上一点,当AM⊥PM时,求出点P的坐标.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)(11,0)
;(3)(11,0)
【解析】试题分析: (1)根据一次函数y=k1x+b的图像经过A、B可得b、k1的方程组,进而求得一次函数的解析式,设M(m,n)作MD⊥x轴于点D,由△OBM的面积为2可求出n的值,将M(m,4)代入y=2x-2求出m的值,由M点在双曲线上求出k2,进而得到反比例函数的解析式;
(2)根据已知构造直角三角形进而利用勾股定理求出AM的长;
(3)过点M作MP⊥AM交x轴于点P,由MD⊥BP求出∠PMD=∠MBD=∠ABO,再由锐角三角形函数的定义求出OP的值,进而可得出结论.
试题解析:(1)∵直线![]() 的图象经过
的图象经过![]() 、
、![]() 两点
两点
∴![]() ,
,
∴解得: ![]()
∴一次函数的表达式为![]() ,
,
∴设![]() ,作MD⊥x轴于点D
,作MD⊥x轴于点D
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴n=4,
∴将![]() 代入
代入![]() 得
得![]() ,
,
∴m=3
∵![]() 在双曲线
在双曲线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴反比例函数的表达式为: ![]() ;
;
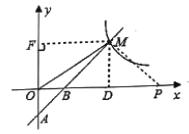
(2)过点M作MF⊥y轴于点F,
则FM=3,AF=4+2=6,
∴![]() ;
;
(3)过点![]() 作MP⊥AM交x轴于点P,
作MP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠PMD=∠MBD=∠ABO
∴![]() ,
,
∴在Rt△PDM中, ![]() ,
,
∴PD=2MD=8,
∴OP=OD+PD=11
∴当PM⊥AM,此时点P的坐标为(11,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
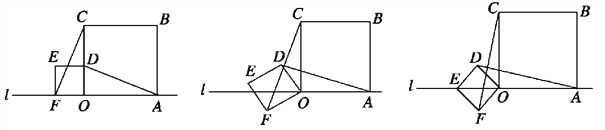
【题目】小明在数学活动课上,将边长为![]() 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a、b(![]() >
>![]() )的正方形纸片叠放在一起.(用含有a、b的代数式表示问题的结果)
)的正方形纸片叠放在一起.(用含有a、b的代数式表示问题的结果)
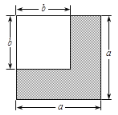
⑴请用至少两种方法求出图中阴影部分的面积;
⑵ 由面积相等,你发现了怎样的等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班为“壮丽70年,奋斗新时代”演讲比赛购买A,B两种奖品.已知A奖品每件x元,B奖品每件y元.
⑴ 若购买A奖品m件,B奖品n件,共需要多少元;
⑵ 设购买A奖品m件,购买A,B两种奖品共10件:
① 购买两种奖品共需要多少元;
② 若购买A奖品至少2件,B奖品至少6件,请设计出购买方案,并说明每种方案的共需要多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,萧山区大力发展旅游业,跨湖桥遗址、湘湖二期三期、宋城千古情、河上民俗、大美进化……这些名词,相信同学们都耳熟能详了,因此近年来,我区的年游客接待量呈逐年稳步上升,2015年接待1800万人次,2015——2017年这三年累计接待游客高达5958万人次.
(1)求萧山区2015——2017年年游客接待量的年平均增长率.
(2)若继续呈该趋势增长,请预测2018年年游客接待量(近似到万人次).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com