Question

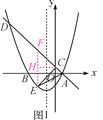
【题目】如图1，在平面直角坐标系中，直线y＝－x＋1与抛物线y＝ax2＋bx＋c(a≠0)相交于点A(1，0)和点D(－4，5)，并与y轴交于点C，抛物线的对称轴为直线x＝－1，且抛物线与x轴交于另一点B.

(1)求该抛物线的函数表达式；

(2)若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；

(3)如图2，若点M是直线x＝－1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．

Answer 1

【答案】(1)抛物线的表达式为y＝x2＋2x－3；(2)△ACE的面积的最大值为；(3)当点M的坐标为(－1，26)或(－1，16)或(－1，8)时，以点A，D，M，N为顶点的四边形能成为平行四边形．

【解析】试题分析：（1）先利用抛物线的对称性确定出点B的坐标，然后设抛物线的解析式为y=a（x+3）（x-1），将点D的坐标代入求得a的值即可；

（2）过点E作EF∥y轴，交AD与点F，过点C作CH⊥EF，垂足为H．设点E（m，m2+2m-3），则F（m，-m+1），则EF=-m2-3m+4，然后依据△ACE的面积=△EFA的面积-△EFC的面积列出三角形的面积与m的函数关系式，然后利用二次函数的性质求得△ACE的最大值即可；

（3）当AD为平行四边形的对角线时．设点M的坐标为（-1，a），点N的坐标为（x，y），利用平行四边形对角线互相平分的性质可求得x的值，然后将x=-2代入求得对应的y值，然后依据＝，可求得a的值；当AD为平行四边形的边时．设点M的坐标为（-1，a）．则点N的坐标为（-6，a+5）或（4，a-5），将点N的坐标代入抛物线的解析式可求得a的值．

试题解析：(1)∴A(1，0)，抛物线的对称轴为直线x＝－1，

∴B(－3，0)，

设抛物线的表达式为y＝a(x＋3)(x－1)，

将点D(－4，5)代入，得5a＝5，解得a＝1，

∴抛物线的表达式为y＝x2＋2x－3；

(2)过点E作EF∥y轴，交AD与点F，交x轴于点G，过点C作CH⊥EF，垂足为H.

设点E(m，m2＋2m－3)，则F(m，－m＋1)．

∴EF＝－m＋1－m2－2m＋3＝－m2－3m＋4.

∴S△ACE＝S△EFA－S△EFC＝EF·AG－EF·HC＝EF·OA＝－ (m＋)2＋.

∴△ACE的面积的最大值为；

(3)当AD为平行四边形的对角线时：

设点M的坐标为(－1，a)，点N的坐标为(x，y)．

∴平行四边形的对角线互相平分，

∴＝， ＝，

解得x＝－2，y＝5－a，

将点N的坐标代入抛物线的表达式，得5－a＝－3，

解得a＝8，

∴点M的坐标为(－1，8)，

当AD为平行四边形的边时：

设点M的坐标为(－1，a)，则点N的坐标为(－6，a＋5)或(4，a－5)，

∴将x＝－6，y＝a＋5代入抛物线的表达式，得a＋5＝36－12－3，解得a＝16，

∴M(－1，16)，

将x＝4，y＝a－5代入抛物线的表达式，得a－5＝16＋8－3，解得a＝26，

∴M(－1，26)，

综上所述，当点M的坐标为(－1，26)或(－1，16)或(－1，8)时，以点A，D，M，N为顶点的四边形能成为平行四边形．