Question

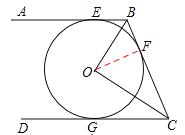
【题目】如图，AB，BC，CD分别与⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm．

（1）求证：BO⊥CO；

（2）求BE和CG的长．

Answer 1

【答案】（1）证明见解析；（2）6.4cm．

【解析】

试题分析：（1）由AB∥CD得出∠ABC+∠BCD=180°，根据切线长定理得出OB、OC平分∠EBF和∠BCG，也就得出了∠OBC+∠OCB=（∠ABC+∠DCB）=×180°=90°．从而证得∠BOC是个直角，从而得出BO⊥CO；

（2）根据勾股定理求得AB=10cm，根据RT△BOF∽RT△BCO得出BF=3.6cm，根据切线长定理得出BE=BF=3.6cm，CG=CF，从而求得BE和CG的长．

试题解析：解：（1）证明：∵AB∥CD，∴∠ABC+∠BCD=180°.

∵AB、BC、CD分别与⊙O相切于E、F、G，∴BO平分∠ABC，CO平分∠DCB.

∴∠OBC=∠ABC，∠OCB=∠DCB.

∴∠OBC+∠OCB=（∠ABC+∠DCB）=×180°=90°.

∴∠BOC=90°. ∴BO⊥CO．

（2）如答图，连接OF，则OF⊥BC，

∴Rt△BOF∽Rt△BCO. ∴.

∵在RT△BOF中，BO=6cm，CO=8cm，

∴根据勾股定理得，BC=10cm，

∴. ∴BF=3.6cm，

∵AB、BC、CD分别与⊙O相切，∴BE=BF=3.6cm，CG=CF.

∵CF=BC﹣BF=10﹣3.6=6.4cm，∴CG=CF=6.4cm．