
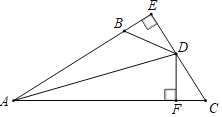
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC.
(2)已知AC=14,BE=2,求AB的长.
【答案】(1)证明见解析;(2)AB=10.
【解析】
(1)求出∠E=∠DFC=90°,根据全等三角形的判定定理得出Rt△BED≌Rt△CFD,推出DE=DF,根据角平分线性质得出即可;
(2)根据全等三角形的性质得出AE=AF,由线段的和差关系求出答案.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴BD=CD,BE=CF,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF,
∵AB=AE﹣BE=AF﹣BE=AC﹣CF﹣BE,
∴AB=14﹣2﹣2=10.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.
(1)求a,b的值;(2)请计算这道题的正确结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=![]() (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
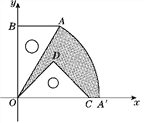
【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3![]() .
.
(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
【答案】(1)反比例函数的解析式为y=![]() ;(2)S阴影=6π-
;(2)S阴影=6π-![]() .
.
【解析】分析:(1)根据tan30°=![]() ,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=
,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=![]() ,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
本题解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴点A的坐标为(3,3![]() ).
).
设反比例函数的解析式为y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,则这个反比例函数的解析式为y=
,则这个反比例函数的解析式为y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由题意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S阴影=S扇形AOA′-S△ODC=6π-![]() .
.
点睛:本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质,本题属于中档题,难度不大,将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
26
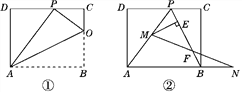
【题目】矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O,连接AP,OP,OA.
① 求证:△OCP∽△PDA;
② 若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南建省30年来,各项事业取得令人瞩目的成就,以2016年为例,全省社会固定资产总投资约3730亿元,其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目.图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图,请完成下列问题:
(1)在图1中,先计算地(市)属项目投资额为 亿元,然后将条形统计图补充完整;
(2)在图2中,县(市)属项目部分所占百分比为m%、对应的圆心角为β,则m= ,β= 度(m、β均取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全相同的4个小球,上面分别标有数字1、-1、2、-2,将其放入一个不透明的盒子中摇匀,再从中随机摸球两次(第一次摸出球后放回摇匀).把第一次、第二次摸到的球上标有的数字分别记作![]() ,
,![]() ,以
,以![]() ,
,![]() 分别作为一个点的横坐标与纵坐标,定义点
分别作为一个点的横坐标与纵坐标,定义点![]() 在反比例函数
在反比例函数![]() 上为事件
上为事件![]() (
(![]() 为整数),当
为整数),当![]() 的概率最大时,则
的概率最大时,则![]() 的所有可能的值为__________.
的所有可能的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国家大力提倡从纯燃油汽车向新能源汽车转型.某汽车制造企业推出了一款新型油电混合动力汽车(在行驶过程中,既可以使用汽油驱动汽年,也可以使用电力驱动汽车,汽油驱动和电力驱动不同时工作).经试验,该型汽车从甲地驶向乙地,只用汽油进行驱动,费用为56元,只用电力进行驱动,费用为20元.已知每行驶1千米,只用汽油驱动的费用比只用电力驱动的费用多0.36元.
(1)求每行驶1千米,只用汽油驱动的费用.
(2)要使从甲地到乙地所需要的燃油费用和电力费用不超过38元,则至少要用电力驱动行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com