
【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=![]() (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
【答案】C
【解析】
过A作AM⊥x轴于M,过B作BN⊥x轴于N,根据菱形性质得出OA=BC=AB=OC,AB∥OC,OA∥BC,求出∠AOM=∠BCN,OM=3,AM=4,OC=OA=AB=BC=5,证△AOM≌△BCN,求出BN=AM=4,CN=OM=3,ON=8,求出B点的坐标,把B的坐标代入y=kx求出k即可.
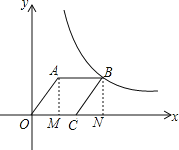
过A作AM⊥x轴于M,过B作BN⊥x轴于N,
则∠AMO=∠BNC=90°,
∵四边形AOCB是菱形,
∴OA=BC=AB=OC,AB∥OC,OA∥BC,
∴∠AOM=∠BCN,
∵A(3,4),
∴OM=3,AM=4,由勾股定理得:OA=5,
即OC=OA=AB=BC=5,
在△AOM和△BCN中
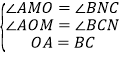 ,
,
∴△AOM≌△BCN(AAS),
∴BN=AM=4,CN=OM=3,
∴ON=5+3=8,
即B点的坐标是(8,4),
把B的坐标代入y=kx得:k=32,
即y=![]() ,
,
故答案选C.


科目:初中数学 来源: 题型:
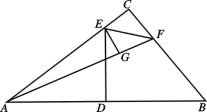
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,垂足是D,F是BC上一点,EF平分∠AFC,EG⊥AF于点G.
(1)试判断EC与EG,CF与GF是否相等;(直接写出结果,不要求证明)
(2)求证:AG=BC;
(3)若AB=5,AF+BF=6,求EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
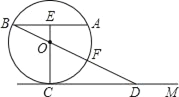
【题目】如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
①求证:EC⊥CD;
②当EO:OC=1:3,CD=4时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程.
(1)x2﹣14x=8(配方法)
(2)x2﹣7x﹣18=0(公式法)
(3)(2x+3)2=4(2x+3)(因式分解法)
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的三个顶点的坐标分别为(2,1),(﹣1,3),(﹣3,2).
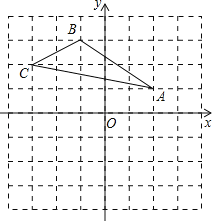
(1)在图中作出△ABC关于x轴对称的△A′B′C′,并写出点A′的坐标为 ,点B的坐标为 ,点C′的坐标为 ;
(2)求△ABC的面积;
(3)若点P(a,a﹣2)与点Q关于y轴对称,若PQ=8,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com