
【题目】如图,在![]() 、
、![]() 上各取一点E、D,使
上各取一点E、D,使![]() ,连接
,连接![]() 、
、![]() 相交于点O,再连接
相交于点O,再连接![]() 、
、![]() ,若
,若![]() ,则图中全等三角形共有( )
,则图中全等三角形共有( )
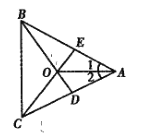
A.2对B.3对C.4对D.5对
【答案】D
【解析】
认真观察图形,确定已知条件在图形上的位置,结合全等三角形的判定方法,由易到难,仔细寻找即可.
①在△AEO与△ADO中,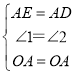 ,
,
∴△AEO≌△ADO(SAS);
②∵△AEO≌△ADO,
∴OE=OD,∠AEO=∠ADO,
∴∠BEO=∠CDO,
在△BEO与△CDO中,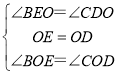 ,
,
∴△BEO≌△CDO(ASA);
③∵△BEO≌△CDO,
∴BE=CD,BO=CO,OE=OD,
∴CE=BD,
在△BEC与△CDB中,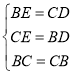 ,
,
∴△BEC≌△CDB(SSS);
④在△AEC与△ADB中,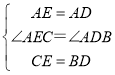 ,
,
∴△AEC≌△ADB(SAS);
⑤∵△AEC≌△ADB,
∴AB=AC,
在△AOB与△AOC中,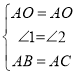 ,
,
∴△AOB≌△AOC(SAS).
综上所述,图中全等三角形共5对.
故选:D.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=![]() (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全相同的4个小球,上面分别标有数字1、-1、2、-2,将其放入一个不透明的盒子中摇匀,再从中随机摸球两次(第一次摸出球后放回摇匀).把第一次、第二次摸到的球上标有的数字分别记作![]() ,
,![]() ,以
,以![]() ,
,![]() 分别作为一个点的横坐标与纵坐标,定义点
分别作为一个点的横坐标与纵坐标,定义点![]() 在反比例函数
在反比例函数![]() 上为事件
上为事件![]() (
(![]() 为整数),当
为整数),当![]() 的概率最大时,则
的概率最大时,则![]() 的所有可能的值为__________.
的所有可能的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.

(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论,_____________.
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度![]() ,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
(3)将图1中的正方形CDEF,绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,得到如图3的情形,点
,得到如图3的情形,点![]() 恰好落在斜边
恰好落在斜边![]() 上,若
上,若![]() ,求正方形CDEF的边长.
,求正方形CDEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国家大力提倡从纯燃油汽车向新能源汽车转型.某汽车制造企业推出了一款新型油电混合动力汽车(在行驶过程中,既可以使用汽油驱动汽年,也可以使用电力驱动汽车,汽油驱动和电力驱动不同时工作).经试验,该型汽车从甲地驶向乙地,只用汽油进行驱动,费用为56元,只用电力进行驱动,费用为20元.已知每行驶1千米,只用汽油驱动的费用比只用电力驱动的费用多0.36元.
(1)求每行驶1千米,只用汽油驱动的费用.
(2)要使从甲地到乙地所需要的燃油费用和电力费用不超过38元,则至少要用电力驱动行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
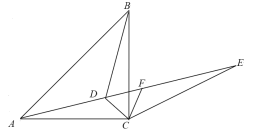
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD.
(1)求证:CD平分∠ACB;
(2)点E是AD延长线上一点,CE=CA,CF∥BD交AE于点F,若∠CAD=15°,
求证:EF=BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com