
【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

【答案】证明见解析,∠BAD=18°
【解析】特例探究:利用等边三角形的三条边都相等、三个内角都是60°的性质推知AB=AC,∠DBA=∠EAC=60°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE.
归纳证明:△ABD与△CAE全等.利用等边三角形的三条边都相等、三个内角都是60°的性质以及三角形外角定理推知AB=AC,∠DBA=∠EAC=120°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE;
拓展应用:利用全等三角形(△ABD≌△CAE)的对应角∠BDA=∠AEC=32°,然后由三角形的外角定理求得∠BAD的度数.
解:特例探究:
证明:∵△ABC是等边三角形,
∴AB=AC,∠DBA=∠EAC=60°,
在△ABD与△CAE中,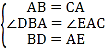 ,
,
∴△ABD≌△CAE(SAS);
归纳证明:
△ABD与△CAE全等.理由如下:
∵在等边△ABC中,AB=AC,∠ABC=∠BAC=60°,
∴∠DBA=∠EAC=120°.
在△ABD与△CAE中,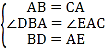 ,
,
∴△ABD≌△CAE(SAS);
拓展应用:
∵点O在AB的垂直平分线上,
∴OA=OB,
∴∠OBA=∠BAC=50°,
∴∠EAC=∠DBC.
在△ABD与△CAE中,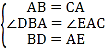 ,
,
∴△ABD≌△CAE(SAS),
∴∠BDA=∠AEC=32°,
∴∠BAD=∠OBA﹣∠BDA=18°.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的三个顶点的坐标分别为(2,1),(﹣1,3),(﹣3,2).
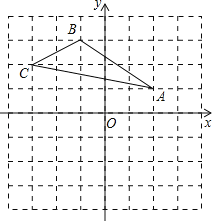
(1)在图中作出△ABC关于x轴对称的△A′B′C′,并写出点A′的坐标为 ,点B的坐标为 ,点C′的坐标为 ;
(2)求△ABC的面积;
(3)若点P(a,a﹣2)与点Q关于y轴对称,若PQ=8,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BCD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AB的垂直平分线MD交AC于点D,AB于M,以下结论:①△BCD是等腰三角形;②射线BD是△ACB的角平分线;③△BCD的周长C△BCD=AC+BC;④△ADM≌BCD.正确的有( )
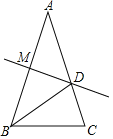
A.①②③B.①②C.①③D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com