
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的袋数是运往
地的袋数是运往![]() 地袋数的3倍,各地的运费如下表所示:
地袋数的3倍,各地的运费如下表所示:
运往地 |
|
|
|
运费(元/袋) | 20 | 10 | 15 |

(1)设运往![]() 地的小米为
地的小米为![]() (袋),总运费为
(袋),总运费为![]() (元),试写出
(元),试写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若总运费不超过14000元,最多可运往![]() 地多少袋小米?
地多少袋小米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,![]() ,
,![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为4,请求出图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,D(0,-3),M(4,-3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系:______.
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
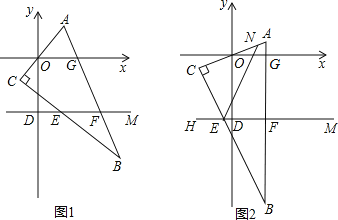
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车的行驶时间为x(h),两车之间的距离为s(km),y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.
(1)图中的a= ,b= .
(2)从甲地到乙地依次有E,F两个加油站,相距200km,若慢车经过E加油站时,快车恰好经过F加油站,求F加油站到甲地的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正数![]() ,用符号
,用符号![]() 表示
表示![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ,
,![]() .点
.点![]() 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于![]() 轴的边长为
轴的边长为![]() ,垂直于
,垂直于![]() 轴的边长为
轴的边长为![]() ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点![]() 的矩形域是一个以
的矩形域是一个以![]() 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.


图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是 ;
(2)点![]() 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求![]() 的值;
的值;
(3)已知点![]() 在直线
在直线![]() 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积![]() 满足
满足![]() ,那么
,那么![]() 的取值范围是 .(直接写出结果)
的取值范围是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com