
【题目】如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=_____°.
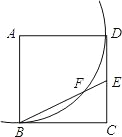
【答案】45
【解析】
由四边形ABCD为正方形及半径相等得到AB=AF=AD,∠ABD=∠ADB=45°,利用等边对等角得到两对角相等,由四边形ABFD的内角和为360度,得到四个角之和为270,利用等量代换得到∠ABF+∠ADF=135°,进而确定出∠1+∠2=45°,由∠EFD为三角形DEF的外角,利用外角性质即可求出∠EFD的度数.
∵正方形ABCD,AF,AB,AD为圆A半径,
∴AB=AF=AD,∠ABD=∠ADB=45°,
∴∠ABF=∠AFB,∠AFD=∠ADF,
∵四边形ABFD内角和为360°,∠BAD=90°,
∴∠ABF+∠AFB+∠AFD+∠ADF=270°,
∴∠ABF+∠ADF=135°,
∵∠ABD=∠ADB=45°,即∠ABD+∠ADB=90°,
∴∠1+∠2=135°90°=45°,
∵∠EFD为△DEF的外角,
∴∠EFD=∠1+∠2=45°.
故答案为:45


科目:初中数学 来源: 题型:
【题目】海南建省30年来,各项事业取得令人瞩目的成就,以2016年为例,全省社会固定资产总投资约3730亿元,其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目.图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图,请完成下列问题:
(1)在图1中,先计算地(市)属项目投资额为 亿元,然后将条形统计图补充完整;
(2)在图2中,县(市)属项目部分所占百分比为m%、对应的圆心角为β,则m= ,β= 度(m、β均取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.

(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论,_____________.
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度![]() ,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
(3)将图1中的正方形CDEF,绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,得到如图3的情形,点
,得到如图3的情形,点![]() 恰好落在斜边
恰好落在斜边![]() 上,若
上,若![]() ,求正方形CDEF的边长.
,求正方形CDEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法一定正确的是( )
A.所有的等边三角形都是全等三角形
B.全等三角形是指形状相同的两个三角形
C.全等三角形是指面积相等的两个三角形
D.全等三角形的周长和面积分别相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国家大力提倡从纯燃油汽车向新能源汽车转型.某汽车制造企业推出了一款新型油电混合动力汽车(在行驶过程中,既可以使用汽油驱动汽年,也可以使用电力驱动汽车,汽油驱动和电力驱动不同时工作).经试验,该型汽车从甲地驶向乙地,只用汽油进行驱动,费用为56元,只用电力进行驱动,费用为20元.已知每行驶1千米,只用汽油驱动的费用比只用电力驱动的费用多0.36元.
(1)求每行驶1千米,只用汽油驱动的费用.
(2)要使从甲地到乙地所需要的燃油费用和电力费用不超过38元,则至少要用电力驱动行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有( )
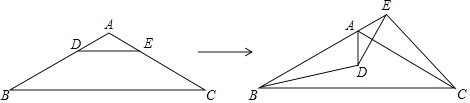
A.②③B.②③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、图2,在圆O中,OA=1,AB=![]() ,将弦AB与弧AB所围成的弓形(包括边界的阴影部分)绕点B顺时针旋转α度(0≤α≤360),点A的对应点是A′.
,将弦AB与弧AB所围成的弓形(包括边界的阴影部分)绕点B顺时针旋转α度(0≤α≤360),点A的对应点是A′.
(1)点O到线段AB的距离是 ;∠AOB= °;点O落在阴影部分(包括边界)时,α的取值范围是 ;
(2)如图3,线段B与优弧ACB的交点是D,当∠A′BA=90°时,说明点D在AO的延长线上;
(3)当直线A′B与圆O相切时,求α的值并求此时点A′运动路径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 、
、![]() 分别在直线
分别在直线![]() 与
与![]() 上,且
上,且![]() ,
,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,若以
,若以![]() 为直径作
为直径作![]() ,则点
,则点![]() 与
与![]() 的位置关系是( )
的位置关系是( )

A. 点P在⊙O外 B. 点P在⊙O内
C. 点P在⊙O上 D. 以上都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com