
【题目】如图1、图2,在圆O中,OA=1,AB=![]() ,将弦AB与弧AB所围成的弓形(包括边界的阴影部分)绕点B顺时针旋转α度(0≤α≤360),点A的对应点是A′.
,将弦AB与弧AB所围成的弓形(包括边界的阴影部分)绕点B顺时针旋转α度(0≤α≤360),点A的对应点是A′.
(1)点O到线段AB的距离是 ;∠AOB= °;点O落在阴影部分(包括边界)时,α的取值范围是 ;
(2)如图3,线段B与优弧ACB的交点是D,当∠A′BA=90°时,说明点D在AO的延长线上;
(3)当直线A′B与圆O相切时,求α的值并求此时点A′运动路径的长度.

【答案】(1)![]() ;120;30°≤α≤60°(2)D在AO的延长线上(3)(3)①α=120°或300°②当α=120°时,A′运动路径的长度=
;120;30°≤α≤60°(2)D在AO的延长线上(3)(3)①α=120°或300°②当α=120°时,A′运动路径的长度=![]() ;当α=300时,A′运动路径的长度=
;当α=300时,A′运动路径的长度=![]() .
.
【解析】
⑴根据垂径定理可得AM=BM=![]() ,在直角三角形中可知O到线段AB的距离,再根据正弦定理,结合圆的性质即可求出答案;(2)利用直径所对的圆周角为直角的性质,得出AD为直径,进而得出点D在AO的延长线上;(3)点A'的运动路径为以B为圆心,AB为半径的圆弧,当直线A'B与圆0相切时,分两种情况,分别计算两种情况下的点A'的运动路径的长度.
,在直角三角形中可知O到线段AB的距离,再根据正弦定理,结合圆的性质即可求出答案;(2)利用直径所对的圆周角为直角的性质,得出AD为直径,进而得出点D在AO的延长线上;(3)点A'的运动路径为以B为圆心,AB为半径的圆弧,当直线A'B与圆0相切时,分两种情况,分别计算两种情况下的点A'的运动路径的长度.
(1)如图1,过点O作OD⊥AB于点D,
由垂径定理知,AD=![]() AB=
AB=![]() ,
,
又OA=1,
∴sin∠AOD=![]() =
=![]() ,
,
∴∠AOD=60°.
∴OD=OAcos60°=![]()
又OA=OB,
∴∠AOB=2∠AOD=120°.
如图2,当A′B与OB重叠时,a=∠OBA=30°;
当OB绕点B顺时针旋转至与圆相交,交点为B′,连接OB′,则OB=OB′=BB′,此时△OBB′是等边三角形,
∴∠OBB′=60°,
∴α的取值范围是:30°≤α≤60°.
故答案是:![]() ;120;30°≤α≤60°;
;120;30°≤α≤60°;
(2)连接AD,∵∠A′BA=90°,
∴AD为直径,
所以D在AO的延长线上;
(3)①当A′B与⊙O相切,
∴∠OBA′=90°,
此时∠ABA′=90°+30°=120°
或∠ABA′=90°﹣30°=60°
∴α=120°或300°
②当α=120°时,
A′运动路径的长度=![]() =
=![]()
当α=300时,
A′运动路径的长度=![]() =
=![]() .
.




 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
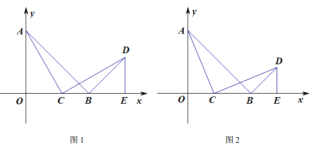
【题目】如图1,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求证:![]() ;
;
(2)猜想![]() 的形状并证明结论;
的形状并证明结论;
(3)如图2,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系中,A点坐标为(0,1),AB=BC=![]() ,∠ABC=90°,CD⊥x轴.
,∠ABC=90°,CD⊥x轴.
(1)填空:B点坐标为 ,C点坐标为 .
(2)若点P是直线CD上第一象限上一点且△PAB的面积为6.5,求P点的坐标;
(3)在(2)的条件下点M是x轴上线段OD之间的一动点,当△PAM为等腰三角形时,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AB的垂直平分线MD交AC于点D,AB于M,以下结论:①△BCD是等腰三角形;②射线BD是△ACB的角平分线;③△BCD的周长C△BCD=AC+BC;④△ADM≌BCD.正确的有( )
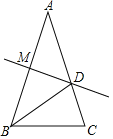
A.①②③B.①②C.①③D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com