【题目】如图，一次函数y1＝kx＋b与二次函数y2＝ax2的图象交于A、B两点．
(1)利用图中条件，求两个函数的解析式；
(2)根据图象写出使y1>y2的x的取值范围．
【答案】（1）一次函数解析式为y1＝x＋2，二次函数解析式为y2＝x2（2）当－1<x<2时，y1>y2.
【解析】
（1）把B坐标代入二次函数解析式即可求得二次函数解析式，把A横坐标代入二次函数解析式即可求得点A坐标；把A，B两点坐标代入一次函数解析式即可求得一次函数的解析式；
（2）应从交点看一次函数的值大于二次函数的值时x的取值．
解：(1)由图象可知：B(2，4)在二次函数y2＝ax2图象上，∴4＝a·22.∴a＝1.则y2＝x2.又∵A(－1，n)在二次函数y2＝x2图象上，∴n＝(－1)2.∴n＝1.则A(－1，1)．又∵A、B两点在一次函数y1＝kx＋b图象上，∴
解得
则y1＝x＋2.∴一次函数解析式为y1＝x＋2，二次函数解析式为y2＝x2.
(2)根据图象可知：当－1<x<2时，y1>y2.
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠CAB=36°，以C为原点，C所在直线为y轴，BC所在直线为x轴建立平面直角坐标系 ，在坐标轴上取一点M使△MAB 为等腰三角形，符合条件的 M 点有（ ）
A.6个B.7个
C.8个D.9个
查看答案和解析>>
科目：初中数学 来源： 题型：
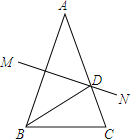
【题目】如图，已知AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D.
(1)求∠DBC的度数.
(2)若△DBC的周长为14cm，BC＝5cm，求AB的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，
其中正确的是（ ）
A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形OABC的顶点A(-8，0)、C(0，6)，点D是BC边上的中点，抛物线y=ax2+bx经过A、D两点，如图所示.
(1)求点D关于y轴的对称点D′的坐标及a、b的值；
(2)在y轴上取一点P,使PA+PD长度最短,求点P的坐标；
(3)将抛物线y=ax2+bx向下平移,记平移后点A的对应点为A1，点D的对应点为D1，当抛物线平移到某个位置时，恰好使得点O是y轴上到A1、D1两点距离之和OA1+OD1最短的一点，求此抛物线的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为弘扬中华民族传统文化，某校举办了“古诗文大赛”，并为获奖同学购买签字笔和笔记本作为奖品．1支签字笔和2个笔记本共8.5元，2支签字笔和3个笔记本共13.5元．
（1）求签字笔和笔记本的单价分别是多少元？
（2）为了激发学生的学习热情，学校决定给每名获奖同学再购买一本文学类图书，如果给每名获奖同学都买一本图书，需要花费720元；书店出台如下促销方案：购买图书总数超过50本可以享受8折优惠．学校如果多买12本，则可以享受优惠且所花钱数与原来相同．问学校获奖的同学有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
为
斜边BC上的高，点E为DA延长线上一点，连结
，过点
作
于点F，交AB、AD于
、
两点.
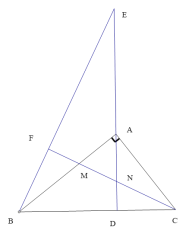
（1）证明：
（2）若
，
，求
的长.
（3）若
，且
，且线段BF与EF的长是关于
的一元二次方程
的两个实数根，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC中，∠CAB=90°，AC=AB=3，△CDE中，∠CDE=90°，CD=DE=5，连接BE，取BE中点F，连接AF、DF．
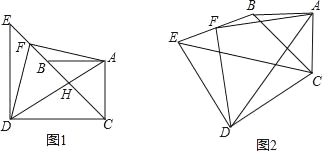
（1）如图1，若C、B、E三点共线，H为BC中点．
①直接指出AF与DF的关系 ；
②直接指出FH的长度 ；
（2）将图（1）中的△CDE绕C点逆时针旋转a（如图2，0°＜α＜180°），试确定AF与DF的关系，并说明理由；
（3）在（2）中，若AF=
，请直接指出点F所经历的路径长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
