
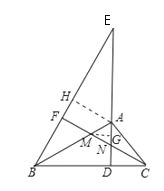
【题目】如图,已知![]() 为
为![]() 斜边BC上的高,点E为DA延长线上一点,连结
斜边BC上的高,点E为DA延长线上一点,连结![]() ,过点
,过点![]() 作
作![]() 于点F,交AB、AD于
于点F,交AB、AD于![]() 、
、![]() 两点.
两点.
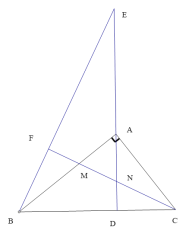
(1)证明:![]()
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)若![]() ,且
,且![]() ,且线段BF与EF的长是关于
,且线段BF与EF的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,求
的两个实数根,求![]() 的长.
的长.
【答案】(1)见解析(2)DE=8.(3)BC=5.
【解析】
(1)判断出△BDE∽△NDC即可证明,
(2)先证明△ADC∽△BDA得到![]() ,即AD2=BDDC,再证明△EBD∽△CND,得到
,即AD2=BDDC,再证明△EBD∽△CND,得到![]() ,故BDDC=EDDN,AD2=EDDN,结合
,故BDDC=EDDN,AD2=EDDN,结合![]() ,
,![]() ,故AD=DN+AN=3,得到32=
,故AD=DN+AN=3,得到32=![]() DE,故可求解;
DE,故可求解;
(3)先证明∠ACM=∠FBM,由(2)可知∠E=∠FCB,∠ABE=∠E,AB=AE
过点M作MG⊥AN于点G,根据MG∥BD得![]() ,由
,由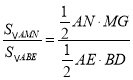 ,得到
,得到![]() ,故
,故![]() ,过点A作AH⊥EF于点H,再由AH∥FN,得
,过点A作AH⊥EF于点H,再由AH∥FN,得![]() ,设EH=8a,则FH=3a,得到BF=5a,EF=11a,由根与系数关系列出方程组解得:a=±
,设EH=8a,则FH=3a,得到BF=5a,EF=11a,由根与系数关系列出方程组解得:a=±![]() ,得到BF=
,得到BF=![]() ,再证明△ACN∽△BCM,得到
,再证明△ACN∽△BCM,得到![]() ,设AC=3b,则BC=5b,在Rt△ABC和 Rt△ACM中,求出MC=
,设AC=3b,则BC=5b,在Rt△ABC和 Rt△ACM中,求出MC=![]() b,再根据△ACM∽△FCB得
b,再根据△ACM∽△FCB得![]() ,得到
,得到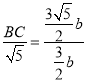 ,即可求解BC.
,即可求解BC.
(1)证明: ∵CF⊥BE,AD⊥CD,
∴∠EFN=∠NDC=90°,
又∠ENF=∠CND,
∴∠E=∠DCN,
又∠EDB=∠EDC=90°,
∴△BDE∽△NDC
∴![]()
故![]()
(2)解:∵∠BAC=90°,AD⊥BC,
∴∠ADC=∠ADB=90°,
∠DAC=∠DBA,
∴△ADC∽△BDA,
∴![]() ,
,
∴AD2=BDDC,
∵CF⊥BE,
∴∠FCB+∠EBD=90°,
∵∠E+∠EBD=90°,
∴∠E=∠FCB,
∵∠NDC=∠EDB=90°,
∴△EBD∽△CND,
∴![]() ,
,
∴BDDC=EDDN,
∴AD2=EDDN,
∵![]() ,
,![]() ,
,
∴AD=DN+AN=3,
∴32=![]() DE,
DE,
∴DE=8.
(3)∵AM=AN,
∴∠AMN=∠ANM
∵∠AMN+∠ACN=90°,∠DNC+∠NCD=90°,
∴∠ACM=∠NCD
∵∠BMF+∠FBM=90°,∠AMC+∠ACM=90°,
∴∠ACM=∠FBM
由(2)可知∠E=∠FCB,
∴∠ABE=∠E,
∴AB=AE
过点M作MG⊥AN于点G
由MG∥BD得![]() ,
,
∴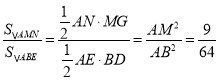 ,
,
∴![]() ,
,
∴![]() ,
,
过点A作AH⊥EF于点H,
由AH∥FN,
得![]() ,
,
设EH=8a,则FH=3a,
∵AE=AB,
∴BH=HE=8a,
∴BF=5a,EF=11a,
由根与系数关系得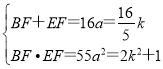 ,
,
解得:a=±![]() ,
,
∵a>0,a=![]() ,
,
∴BF=![]() ,
,
由∠ACM=∠MCB,∠DAC=∠DBA可知△ACN∽△BCM,
∴![]()
设AC=3b,则BC=5b
在Rt△ABC中,有AB=4b.
∴AM=![]() b.
b.
在Rt△ACM中,有MC=![]() b
b
由△ACM∽△FCB得![]() ,∴
,∴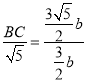 ,
,
∴BC=5.


科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与二次函数y2=ax2的图象交于A、B两点.

(1)利用图中条件,求两个函数的解析式;
(2)根据图象写出使y1>y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)

(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
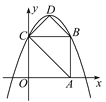
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com