
����Ŀ������OABC�Ķ���A(-8��0)��C(0��6)����D��BC���ϵ��е㣬������y=ax2+bx����A��D���㣬��ͼ��ʾ.
(1)���D����y��ĶԳƵ�D������꼰a��b��ֵ��
(2)��y����ȡһ��P,ʹPA+PD�������,���P�����ꣻ
(3)��������y=ax2+bx����ƽ��,��ƽ�ƺ��A�Ķ�Ӧ��ΪA1����D�Ķ�Ӧ��ΪD1����������ƽ�Ƶ�ij��λ��ʱ��ǡ��ʹ�õ�O��y���ϵ�A1��D1�������֮��OA1+OD1��̵�һ�㣬��������ߵĽ���ʽ.

���𰸡���1��D��(4��6). a=-![]() ,b=-3.��2��P(0��4).��3��y=-
,b=-3.��2��P(0��4).��3��y=-![]() x2-3x-4.
x2-3x-4.
�������������������1�����ȸ��ݾ��ε����ʵõ���B�����꣬Ȼ��õ���D�����꣬�Ӷ��õ���D������꣬Ȼ�����ô���ϵ�������a��b��ֵ���ɣ�
��2�����ֱ��AD��Ľ���ʽ�����ֱ����y��Ľ������꼴Ϊ��P�����ꣻ
��3���������ô���ϵ�������ֱ��A1D1��Ľ���ʽ�����ݵ�OΪʹOA1+OD1��̵ĵ����m��ֵ���Ӷ�ȷ�������ߵĽ���ʽ��
�����������1)�ɾ��ε����ʿ�֪��B(-8��6)����D(-4��6).���D����y��ԳƵ�D��(4��6).
��A(-8��0)��D(-4��6)����y=ax2+bx����64a-8b=0,16a-4b=6.��a=-![]() ,b=-3.
,b=-3.
(2)��ֱ��AD���Ľ���ʽΪy=kx+n����-8k+n=0,4k+n=6.���k=![]() ,n=4.
,n=4.
��ֱ��y=![]() x+4��y�ύ�ڵ�(0��4).��P(0��4).
x+4��y�ύ�ڵ�(0��4).��P(0��4).
(3)�ⷨ1������OP=4���ʽ�����������ƽ��4����λʱ����OA1+OD1���.
��y+4=-![]() x2-3x������ʱ�Ľ���ʽΪy=-
x2-3x������ʱ�Ľ���ʽΪy=-![]() x2-3x-4.
x2-3x-4.
�ⷨ2��������������ƽ����m����λ����A1(-8��-m)��D1(-4��6-m)����D��1��4��6-m��.
��ֱ��A1D��1Ϊy=k��x+b��.��-8k��+b��=-m,4k��+b��=6-m.��k��=![]() ,b��=4-m.
,b��=4-m.
�ߵ�OΪʹOA1+OD1��̵ĵ㣬��b��=4-m=0.��m=4����������������ƽ����4����λ.
��y+4=-![]() x2-3x������ʱ�Ľ���ʽΪy=-
x2-3x������ʱ�Ľ���ʽΪy=-![]() x2-3x-4.
x2-3x-4.


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ�����һЩ�ز�������ǰ��Χ�ơ�A�����а��棬B������᭸ɶ�����C���������ɺ�Ѽ����D���˳Ǻ����ӻ����������ز�����ȫ�з�Χ�������ȡ�˲�����������ʾ����飺������ϲ�����ز���ʲô��������ѡ��ֻѡһ�֣����ֽ��������������Ƴ���ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ��
�����������Ϣ����������⣺
��1���벹ȫ����ͳ��ͼ������ͳ��ͼ��
��2����ȫ����280��������ȫ����ϲ��������᭸ɶ�����������Լ�ж������ˣ�
��3����һ�������Ŀڴ������ĸ��ֱ�д�������ز����A��B��C��D��С���������ȫ��ͬ�����������һ��С��Ȼ��Żأ����ҡ�Ⱥ����������һ��С�������ζ�������A���ĸ���Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
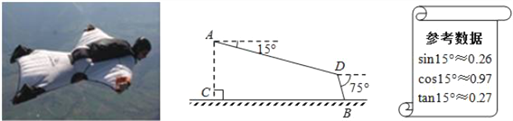
����Ŀ����ͼ,ij��װ����Ա����ˮƽ�����AC=500m��A������,���Ÿ���Ϊ15��ķ���,ֱ����1600����D�㣬Ȼ�����ɡ��75��ĸ��ǽ��䵽�����ϵ�B��.�������е�ˮƽ����BC�������ȷ��1m����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣬��ȷ���ǣ�������
A.4a��2a=2
B.a6��a3=a2
C.����a3b��2=a6b2
D.��a+b��2=a2+b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯Ա���������![]() �ס�������������Ϊ����������Ĺ˿ͣ��ֱ��Ƴ������ε������Żݰ취
�ס�������������Ϊ����������Ĺ˿ͣ��ֱ��Ƴ������ε������Żݰ취![]() ����������Żݰ취�ǣ���4��ȫƱ�������˰�ԭ�۵������շѣ�����������Żݰ취�ǣ�һ�ɰ�ԭ�۵������շ�
����������Żݰ취�ǣ���4��ȫƱ�������˰�ԭ�۵������շѣ�����������Żݰ취�ǣ�һ�ɰ�ԭ�۵������շ�![]() ��֪�������������ԭ�۾�ΪaԪ���������й����еĸ��ַ���������ͬ
��֪�������������ԭ�۾�ΪaԪ���������й����еĸ��ַ���������ͬ![]() ������Ǹù�˾�ĸ����ˣ����ѡ���ļ�������.
������Ǹù�˾�ĸ����ˣ����ѡ���ļ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ƶ�ͨѶ��˾����������ͨѶҵ��: ��ȫ��ͨ�� ʹ�����Ƚ�50Ԫ�»�����, Ȼ��ÿͨ��1����, �ٸ��绰��0.4Ԫ; �������С� �����»�����, ÿͨ��1����, ������0.6Ԫ(�����ָ����ͨ��). ��һ������ͨ��x����, ����ͨѶ��ʽ�ķ��÷ֱ�Ϊy1Ԫ��y2Ԫ.
(1)д��y1��y2��x֮��ĺ�����ϵʽ;
(2)һ������ͨ�����ٷ���, ����ͨѶ��ʽ�ķ�����ͬ?
(3)��ij��Ԥ��һ������ʹ�û���200Ԫ, ��Ӧѡ������ͨѶ��ʽ�Ϻ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��x2��ͼ������ƽ��m��m��0������λ������ƽ��2����λ����ƽ���Ժ�Ķ��κ����Ľ���ʽΪ��������
A.y����x+2��2��mB.y����x+2��2+mC.y����x+m��2+2D.y����x��2��2+m
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com