
【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
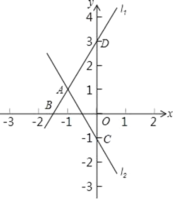
【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A、B、C、D点坐标;
(2)求出直线l2的解析式;
(3)连结BC,求出S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与二次函数y2=ax2的图象交于A、B两点.

(1)利用图中条件,求两个函数的解析式;
(2)根据图象写出使y1>y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)

(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
科目:初中数学 来源: 题型:
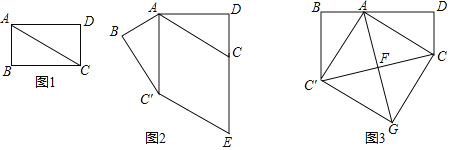
【题目】如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.
(2)若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com