
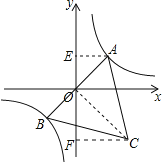
【题目】如图,已知等边三角形![]() 的顶点
的顶点![]() 分别在反比例函数
分别在反比例函数![]() 图像的两个分支上,点
图像的两个分支上,点![]() 在反比例函数
在反比例函数![]() 的图像上,当
的图像上,当![]() 的面积最小时,
的面积最小时,![]() 的值__________.
的值__________.

【答案】-3
【解析】
当等边三角形ABC的边长最小时,△ABC的面积最小,点A,B分别在反比例函数y=![]() 图象的两个分支上,则当A、B在直线y=x上时最短,即此时△ABC的面积最小,根据反比例函数图象的对称性可得OA=OB,设OA=x,则AC=2x,OC=
图象的两个分支上,则当A、B在直线y=x上时最短,即此时△ABC的面积最小,根据反比例函数图象的对称性可得OA=OB,设OA=x,则AC=2x,OC=![]() x,根据等边三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得结论.
x,根据等边三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得结论.
解:根据题意当A、B在直线y=x上时,△ABC的面积最小,
函数y=![]() 图象关于原点对称,
图象关于原点对称,
∴OA=OB,
连接OC,过A作AE⊥y轴于E,过C作CF⊥y轴于F,
∵△ABC是等边三角形,
∴AO⊥OC,
∴∠AOC=90°,∠ACO=30°,
∴∠AOE+∠COF=90°,
设OA=x,则AC=2x,OC=![]() x,
x,
∵AE⊥y轴,CF⊥y轴,
∴∠AEO=∠OFC=∠AOE+∠OAE=90°,
∴∠COF=∠OAE,
∴△AOE∽△OCF,
∴![]() ,
,
∵顶点A在函数y=![]() 图象的分支上,
图象的分支上,
∴S△AOE=![]() ,
,
∴S△OCF=![]() ,
,
∵点C在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=-3,
故答案为-3.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)延长线段![]() 到
到![]() ,延长线段
,延长线段![]() 到
到![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①判断![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
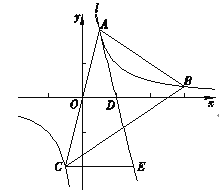
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .已知点
.已知点![]() ,点
,点![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,抛物线的对称轴为直线
两点,抛物线的对称轴为直线![]()
①求![]() ,
,![]() 所满足的数量关系式;
所满足的数量关系式;
②当OP=OA时,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=10,tanA=![]() .点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
.点P是斜边AB上一个动点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A.
B.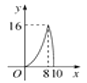
C.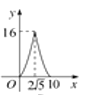
D.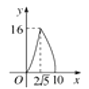
查看答案和解析>>
科目:初中数学 来源: 题型:
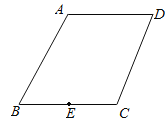
【题目】已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com