
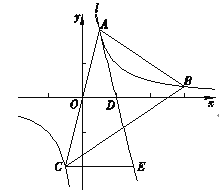
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
【答案】(1)m=1;y=-4x+4;(2)E(![]() ,-2);(3)证明见解析.
,-2);(3)证明见解析.
【解析】试题分析:(1)将点A(![]() ,2)代入
,2)代入![]() 求出m的值,再将A(
求出m的值,再将A(![]() ,2),D(1,0)分别代入y=kx+b,求出k、b的值;
,2),D(1,0)分别代入y=kx+b,求出k、b的值;
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2),由yE=yC求出E点坐标.
,﹣2),由yE=yC求出E点坐标.
(3)作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,由于点B(3,n)在反比例函数图象上,求出n=![]() ,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
试题解析:解:(1)∵点A(![]() ,2)在反比例函数
,2)在反比例函数![]() (m为常数)的图象上,∴m=
(m为常数)的图象上,∴m=![]() ×2=1,∴反比例函数
×2=1,∴反比例函数![]() (m为常数)对应的函数表达式是
(m为常数)对应的函数表达式是![]() .
.
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A(![]() ,2),D(1,0),∴
,2),D(1,0),∴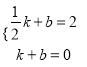 ,解得:
,解得: ![]() ,∴直线l对应的函数表达式为y=﹣4x+4.
,∴直线l对应的函数表达式为y=﹣4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2).
,﹣2).
∵CE∥x轴交直线l于点E,∴yE=yC,∴点E的坐标为E(![]() ,﹣2).
,﹣2).
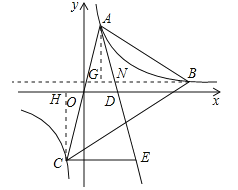
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,∵点B(3,n)在反比例函数图象上,∴n=![]() ,∴B(3,
,∴B(3, ![]() ),G(
),G(![]() ,
, ![]() ),H(﹣
),H(﹣![]() ,
, ![]() ).
).
在Rt△ABG中,tan∠ABH= ,在Rt△BCH中,tan∠CBH=
,在Rt△BCH中,tan∠CBH= ,∴tan∠ABN=tan∠CBN.
,∴tan∠ABN=tan∠CBN.


科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
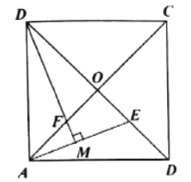
【题目】如图,正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
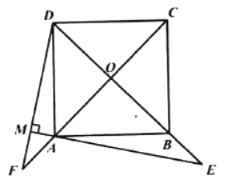
(1) (2)
(1)若点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(2)若点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,其他条件不变结论“
,其他条件不变结论“![]() ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④![]() 。其中正确的结论有( )
。其中正确的结论有( )
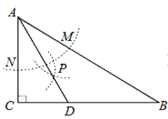
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
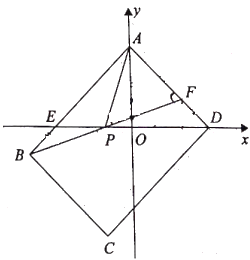
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 延长线上任意一点,以
延长线上任意一点,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,且
,且![]() ,连结
,连结![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )在点
)在点![]() 运动过程中,试问
运动过程中,试问![]() 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
(![]() )已知
)已知![]() ,设
,设![]() ,
, ![]() .
.
①试求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
②当![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() .
.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com