
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
【答案】y=x2﹣2x﹣3.
【解析】先求出y=x2-2x+1和y=2x-2的交点C′的坐标为(1,4),再求出“梦之星”抛物线y=x2+2x+1的顶点A坐标(-1,0),接着利用点C和点C′关于x轴对称得到C(1,-4),则可设顶点式y=a(x-1)2-4然后把A点代入求出a的值即可得到原抛物线解析式.
解:∵y=x2-2x+1=(x+1)2,∴点A的坐标为(-1,0),
解方程组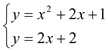 得
得![]() 或
或![]() ,
,
∴C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
C(1,-4),
设原抛物线的解析式为y=a(x-1)2-4,
把A(-1,0)代入求得4a-4=0,解得a=1,
∴原抛物线的解析式为y=a(x-1)2-4=x2-2x-3.
故答案为:y= x2-2x-3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分8分) 已知:如图,在正方形ABCD中,F是AB上一点,延长CB到E,使BE=BF,连接CF并延长交AE于G.
(1)求证:△ABE≌△CBF;
(2)将△ABE绕点A逆时针旋转90°得到△ADH,请判断四边形AFCH是什么特殊四边形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形,并探究和解答下列问题:

(1)设铺设地面所用瓷砖的总块数为y,请写出y与n(表示第n个图形)的关系式;
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明
查看答案和解析>>
科目:初中数学 来源: 题型:
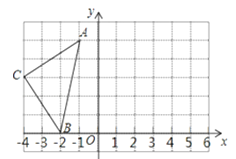
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A'B′C′(其中A'、B′、C′分别是A、B、C的对称点,不写画法);
(2)写出C′的坐标,并求△ABC的面积;
(3)在y轴上找出点P的位置,使线段PA+PB的最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com